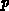 -body (channel region) and the
-body (channel region) and the 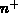 -source
region. Moreover, the channel MOSFET model allows a continuous description
of all operational regimes.
-source
region. Moreover, the channel MOSFET model allows a continuous description
of all operational regimes.




A compact model for circuit simulation for the vertical DMOS-transistor has been developed. For the sake of flexibility, a subcircuit approach has been chosen. On the one hand, the number of elements in the subcircuit has been minimized in order to keep simulation times low also for complex circuits with many DMOS-transistors. On the other hand, the models of the elements in the subcircuit have been adapted to the special structure of the DMOS-transistor in order to achieve the highest possible accuracy. The model has been implemented into the circuit simulator SABER.
The fact that all model parameters in a physically based compact model have a physical meaning (in contrast to an empirical model, a purely mathematical fitting model) is of advantage for fitting the parameters as well as for the circuit simulations themselves. Some parameters have well known values, the others, which are not exactly known (mobilities, series resistances, ...), have well defined initial values and allowed ranges for an optimization, which can speed up the fitting procedure essentially. Physically meaningful parameters allow worst case and sensitivity analysis in the circuit simulation.
In order to identify and extract the important physical effects in the DMOS-transistor, extensive device simulations with MINIMOS have been performed. The possibility to analyze the distribution of the important quantities inside the device led to a subcircuit consisting of a MOSFET model for the channel of the DMOS-transistor, and a JFET-like model, which together with a resistor-like model describes the drift region. Two bipolar transistor models are used for the description of the device behavior under reverse bias conditions.
The MOSFET model for the channel has been adapted to the DMOS-structure by
taking into account the strongly nonuniform channel doping in lateral
direction (in the direction of current flow in the channel). This is typical
for a DMOS-transistor as the channel doping is defined by the different
lateral outdiffusions of the 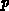 -body (channel region) and the
-body (channel region) and the 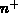 -source
region. Moreover, the channel MOSFET model allows a continuous description
of all operational regimes.
-source
region. Moreover, the channel MOSFET model allows a continuous description
of all operational regimes.
The JFET-like model for the drift region takes into account both the
(small) pinching of the current flow between the 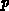 -bodies of adjacent
DMOS-cells and the very important drift velocity saturation in this region.
The resistor-like model describes the current spreading effect between the
JFET-region and the buried layer, which forms the drain region.
-bodies of adjacent
DMOS-cells and the very important drift velocity saturation in this region.
The resistor-like model describes the current spreading effect between the
JFET-region and the buried layer, which forms the drain region.
As the gate electrode is extended over the drift region between adjacent DMOS-cells, an important additional input capacitance has to be modeled. The DMOS-model offers two levels of sophistication for this task. If capacitances are only of interest for positive gate voltages, an explicit model can be used. A very good description of this additional input capacitance for all terminal voltages is given by the second, implicit model, which is based on the calculation of the implicitly given surface potential of the drift region. The circuit simulator of our choice, SABER, automatically adds a virtual node to the matrix of the nonlinear iteration process and is therefore able to calculate this capacitance with only slightly increased iteration numbers.
Besides the advantage of a low area consumption in comparison with comparable lateral transistors, the vertical concept of the DMOS-transistor also gives the possibility to widely vary the on-resistance by changing the number of parallel cells. As the models of the elements of the DMOS-subcircuit are physically based and therefore include the characteristic dimensions of the DMOS-transistor as model parameters, the DMOS-model was easily extended to take into account a varying number of cells. All model parameters (except for those, which determine the number of cells) are independent from the number of the cells of the DMOS-transistor.
With the help of some representative circuits, comparisons of circuit simulations incorporating the DMOS-model and measurements show that the DC- as well as the AC-description and the scalability of the model give good results.



