Dieses Durchbruchphänomen ist sehr ähnlich dem gerade besprochenen, jedoch ist es mit dem body bias effect bei MOSFETs verbunden [8][51]. Der sog. body-Faktor wird hier als
mit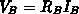 
(vgl. Abb. 4.3) definiert. In [51] ist
ein analytischer Ausdruck für 
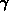angegeben. Wesentlich dabei ist,
daß wie bei einem klassischen MOSFET auch hier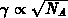 
gilt.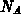 
ist die Dotierungskonzentration des 
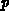-bodies.
Der Sourcestrom im Ersatzschaltbild in Abb. 4.3 ergibt sich (bei ausgeschaltetem parasitärem Bipolartransistor) zu:
Der bei Lawinengeneration entstehende Strom erzeugt an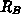 
eine Spannung
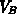, die über den body-Faktor zum Transistorstrom einen Beitrag
leistet. Mit dem Multiplikationsfaktor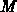 
ergibt sich der body-Strom
zu:
Daraus folgen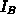 
und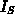 
:
Mit Hilfe von Gleichung 4.1 kann die snapback-Spannung für diesen Effekt berechnet werden:
Man sieht, daß die snapback-Spannung wiederum verkehrt proportional zum Basiswiderstand ist. Im Gegensatz zum sekundären Bipolardurchbruch ist hier der parasitäre Bipolartransistor aber ausgeschaltet.
