


Next: 5. Ausblick
Up: 4. Transportberechnung
Previous: 4.2 Monte Carlo-Methode
Um den Mittelwert einer Größe
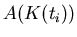 im Monte Carlo Programm zu bestimmen, wird die so genannte
,,before-scattering`` Methode verwendet [18].
im Monte Carlo Programm zu bestimmen, wird die so genannte
,,before-scattering`` Methode verwendet [18].
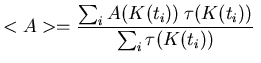 , , 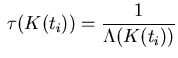 |
(4.41) |
Dabei ist 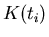 der Betrag des Impulses unmittelbar vor dem
der Betrag des Impulses unmittelbar vor dem 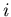 -ten Streuprozess, der zum Zeitpunkt
-ten Streuprozess, der zum Zeitpunkt 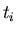 stattfindet.
stattfindet.
Die betrachteten physikalischen Größen im folgenden Beispiel sind:
- Geschwindigkeit
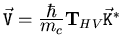
- Energie des Elektrons relativ zum Subbandminimum.
Bei der Ermittlung statistischer Daten zu einer gewissen Talsorte
dürfen die Summen in 4.41 nur über jene
Zeitpunkte erstreckt werden, zu denen sich das Elektron in der
betreffenden Talsorte befindet.
Die mittlere Besetzungszahl 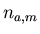 wird aus der Summe der freien
Flugzeiten
wird aus der Summe der freien
Flugzeiten 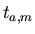 , die sich das Elektron im
Subband
, die sich das Elektron im
Subband 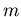 von Tal
von Tal 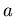 befindet, und der Summe aller
freien Flugzeiten
befindet, und der Summe aller
freien Flugzeiten 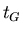 berechnet.
berechnet.
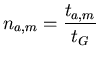 |
(4.42) |
Abbildung 4.8:
Driftgeschwindigkeit als Funktion des Parallelfeldes.
|
|
Abbildung 4.9:
Umbesetzung der Talsorten als Funktion des Parallelfeldes.
|
|
Abbildung 4.10:
Mittlere Energie in den verschiedenen Talsorten als
Funktion des Parallelfeldes.
|
|
Abbildung 4.8 zeigt die resultierende
Driftgeschwindigkeit in der Richtung des Ladungstransports unter
Berücksichtigung von akustischer Deformationspotenzialstreuung und der
Zwischentalstreuung. Die Eingangsparameter wie die effektiven Weiten
und Eigenenergien wurden aus der selbstkonsistenten Lösung für eine
MOS-Struktur mit 3 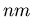 , einer Substratdotierung von
, einer Substratdotierung von
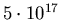
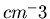 und einer Gate-Bulk-Spannung von
und einer Gate-Bulk-Spannung von
Abbildung 4.11:
Besetzung der Subbänder als Funktion des Parallelfeldes.
|
|
Abbildung 4.12:
Driftgeschwindigkeit in den verschiedenen Talsorten bei
verschiedenen Parallelfeldern.
|
|
1 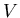 gewonnen.
Die Umbesetzung der Subbänder bei höheren Feldern ist in
Abbildung 4.11 zu sehen. Dort ist die Besetzung der
ersten vier Subbänder über dem Parallelfeld aufgetragen. Bei
schwachem Feld erreichen die Elektronen während dem freien
Flug nicht ausreichend Energie um in energetisch
höher gelegene Subbänder zu streuen.
Nach einem Streuprozess in das erste Subband, der am wahrscheinlichsten ist,
verbleiben die Elektronen daher lang in diesem Subband.
Die mittlere Energie der Ladungsträger in den einzelnen Talsorten ist in
Abbildung 4.10 zu sehen.
In Abbildung 4.12 ist die Driftgeschwindigkeit je
Talsorte über dem Parallelfeld aufgetragen. Talsorte
gewonnen.
Die Umbesetzung der Subbänder bei höheren Feldern ist in
Abbildung 4.11 zu sehen. Dort ist die Besetzung der
ersten vier Subbänder über dem Parallelfeld aufgetragen. Bei
schwachem Feld erreichen die Elektronen während dem freien
Flug nicht ausreichend Energie um in energetisch
höher gelegene Subbänder zu streuen.
Nach einem Streuprozess in das erste Subband, der am wahrscheinlichsten ist,
verbleiben die Elektronen daher lang in diesem Subband.
Die mittlere Energie der Ladungsträger in den einzelnen Talsorten ist in
Abbildung 4.10 zu sehen.
In Abbildung 4.12 ist die Driftgeschwindigkeit je
Talsorte über dem Parallelfeld aufgetragen. Talsorte 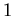 und
und 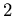 haben die gleiche Masse in
haben die gleiche Masse in 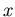 -Richtung, jener Richtung in der das
treibende Feld angelegt wird. Die entsprechenden Subbänder sind jedoch
durch unterschiedliche Quantisierungsmassen entstanden. Talsorte
-Richtung, jener Richtung in der das
treibende Feld angelegt wird. Die entsprechenden Subbänder sind jedoch
durch unterschiedliche Quantisierungsmassen entstanden. Talsorte 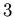 hat die gleiche Quantisierungsmasse wie Subband
hat die gleiche Quantisierungsmasse wie Subband 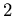 , aber eine andere
Transportmasse wie Talsorte
, aber eine andere
Transportmasse wie Talsorte 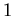 und
und  . Dies erklärt, warum sich drei
verschiedene Verläufe der Driftgeschwindigkeit je Talsorte ergeben.
. Dies erklärt, warum sich drei
verschiedene Verläufe der Driftgeschwindigkeit je Talsorte ergeben.



Next: 5. Ausblick
Up: 4. Transportberechnung
Previous: 4.2 Monte Carlo-Methode
C. Troger: Modellierung von Quantisierungseffekten in Feldeffekttransistoren
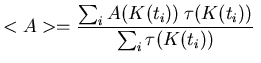 ,
, 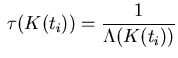
![]() wird aus der Summe der freien
Flugzeiten
wird aus der Summe der freien
Flugzeiten ![]() , die sich das Elektron im
Subband
, die sich das Elektron im
Subband ![]() von Tal
von Tal ![]() befindet, und der Summe aller
freien Flugzeiten
befindet, und der Summe aller
freien Flugzeiten ![]() berechnet.
berechnet.
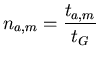
![\includegraphics[]{MC/talv-fin.eps}](img650.png)