previous up next Dissertation Enzo Ungersboeck contents
 Previous: 3.3.3 Strain Resulting from Epitaxy   Up: 3. Strained Bulk Band Structure   Next: 3.4.1 Band Structure of Relaxed Si


3.4 Basic Properties of the Diamond Structure

The structure depicted in Figure 3.4 consists of two basis atoms and may be thought of as two inter-penetrating face centered cubic (fcc) lattices, one displaced from the other by a translation of $ \frac{a_0}{4} (1,1,1)$ along a body diagonal.

Figure 3.4: (a) Crystallographic unit cell (unit cube) of the diamond structure. (b) The primitive basis vectors of the face centered cubic (fcc) lattice and the two atoms forming the basis are highlighted.
[a]\includegraphics[width=2.6in]{inkscape/DiamondLattice.eps} [b]\includegraphics[width=2.45in]{inkscape/DiamondLattice2.eps}

In cubic semiconductors such as Si or Ge the two atoms of the basis are identical and the structure is called the diamond structure. If the two basis atoms are different, the structure is called the zinc-blende structure. Many III-V semiconductors such as GaAs, AlsAs, InAs, or InP are of zinc-blende type.

In Figure 3.4 the diamond structure is depicted. The primitive basis vectors and the two atoms at $ (0,0,0)$ and $ \frac{a_0}{4} (1,1,1)$ are highlighted in Figure 3.4b. The basis vectors of the direct Bravais lattice are

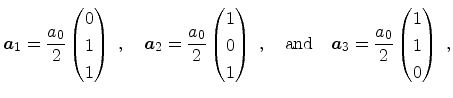$\displaystyle {\ensuremath{\mathitbf{a}}}_1 = \frac{a_0}{2} \begin{pmatrix}0 \\... ...th{\mathitbf{a}}}_3 = \frac{a_0}{2} \begin{pmatrix}1 \\ 1 \\ 0 \end{pmatrix}\ ,$ (3.21)

where $ a_0$ denotes the lattice constant of the relaxed lattice. The lattice is invariant under translations involving lattice vectors of the form

$\displaystyle {\ensuremath{\mathitbf{R}}}_{ijk} = i {\ensuremath{\mathitbf{a}}}_1 + j{\ensuremath{\mathitbf{a}}}_2 + k{\ensuremath{\mathitbf{a}}}_3\ ,$ (3.22)

where $ i,j$ and $ k$ are integers. In the unstrained lattice the distance from the basis atom at $ \frac{a_0}{4} (1,1,1)$ to its four nearest neighbors is given by $ a_0\cdot \sqrt{3}/4$.

The basis vectors of the reciprocal lattice $ \mathitbf{b}$$ _i$ are obtained from the relation $ {\ensuremath{\mathitbf{b}}}_i \cdot {\ensuremath{\mathitbf{a}}}_j = 2\pi \delta_{ij}$ as

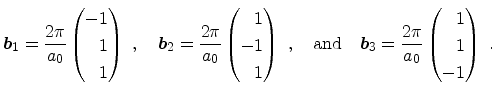$\displaystyle {\ensuremath{\mathitbf{b}}}_1 = \frac{2\pi}{a_0} \begin{pmatrix}-... ...2\pi}{a_0} \begin{pmatrix}\hphantom{-}1 \\ \hphantom{-}1 \\ -1 \end{pmatrix}\ .$ (3.23)

General reciprocal lattice vectors are of the form

$\displaystyle {\ensuremath{\mathitbf{G}}}_{lmn} = l {\ensuremath{\mathitbf{b}}}_1 + m{\ensuremath{\mathitbf{b}}}_2 + n{\ensuremath{\mathitbf{b}}}_3\ ,$ (3.24)

where $ l,m,$ and $ n$ are integers.

The first Brillouin zone (BZ) represents the central (Wigner-Seitz) cell of the reciprocal lattice. It contains all points nearest to the enclosed reciprocal lattice point. The boundaries of the first BZ are determined by planes which are perpendicular to the reciprocal lattice vectors pointing from the center of the cell to the 14 lattice points nearest to the origin of the cell at their midpoints. The 14 faces are

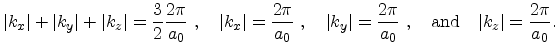$\displaystyle \vert k_x\vert + \vert k_y\vert + \vert k_z\vert = \frac{3}{2} \f... ...= \frac{2\pi}{a_0}\ ,\quad\mathrm{and} \quad \vert k_z\vert = \frac{2\pi}{a_0}.$ (3.25)

Figure 3.5: (a) First Brillouin zone of the fcc lattice. (b) The inset gives the locations of certain symmetry points and symmetry lines in the BZ.
[a]\includegraphics[width=2.6in]{inkscape/bz.eps} [b]\includegraphics[width=2.6in]{inkscape/bzOctand.eps}
In Figure 3.5a the first BZ is depicted. It has a volume $ \Omega_0$ of $ 4 (2\pi/a_0)$ [Singh93].

Due to the translational invariance of the lattice the wave functions and the energy bands are periodic in the reciprocal space and it is sufficient to consider only the first BZ for band structure calculations [Yu03].

The diamond structure is invariant not only under translations, but also under several other symmetry operations such as reflections, rotations, or inversion. These symmetry operations are usually denoted as point operations, since they leave at least one point of the lattice invariant, which is not the case for translations. The set of all point operations for a particular crystal structure forms a group which is denoted as point group. The point group of the diamond structure has 48 symmetry elements which are reflected in the symmetry of the first BZ. A quick examination (see Figure 3.5) shows that the BZ is invariant under various rotations, for example 90$ ^{\circ}$ rotations about the $ {\ensuremath{\mathitbf{k}}}_x$, $ {\ensuremath{\mathitbf{k}}}_y$, and $ {\ensuremath{\mathitbf{k}}}_z$ axes and under reflections through certain planes. A detailed examination of all 48 point symmetries of the unstrained diamond structure will be given in Section 3.5.2.

The point symmetries of the crystal structure are mirrored in the crystal potential, and hence in the one-particle Hamiltonian used for band structure calculations. Two important consequences for the electron band structure arise:

The irreducible wedge of the fcc lattice is depicted in Figure 3.5b. It has six corners

$\displaystyle \Gamma$ $\displaystyle = \frac{2\pi}{a_0} \begin{pmatrix}0 \\ 0 \\ 0 \end{pmatrix},$ $\displaystyle X = \frac{2\pi}{a_0} \begin{pmatrix}1 \\ 0 \\ 0 \end{pmatrix},$   $\displaystyle L = \frac{2\pi}{a_0} \begin{pmatrix}\frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{pmatrix},$    
$\displaystyle W$ $\displaystyle = \frac{2\pi}{a_0} \begin{pmatrix}1 \\ \frac{1}{2} \\ 0 \end{pmatrix},$ $\displaystyle K = \frac{2\pi}{a_0} \begin{pmatrix}\frac{3}{4} \\ \frac{3}{4} \\ 0 \end{pmatrix},$   $\displaystyle U = \frac{2\pi}{a_0} \begin{pmatrix}1 \\ \frac{1}{4} \\ \frac{1}{4} \end{pmatrix},$ (3.26)

connected via symmetry lines

$\displaystyle \Lambda$ $\displaystyle : \Gamma \rightarrow L,$ $\displaystyle \Delta$ $\displaystyle : \Gamma \rightarrow X,$ $\displaystyle S$ $\displaystyle : X \rightarrow U,K,$    
$\displaystyle \Sigma$ $\displaystyle : \Gamma \rightarrow U,K,$ $\displaystyle Q$ $\displaystyle : L \rightarrow W,$ $\displaystyle Z$ $\displaystyle : X \rightarrow W.$ (3.27)

By convention upper case Greek letters are used for points and lines inside the first BZ, whereas roman letters denote points and lines on the surface of the first BZ. Here, the points $ U$ and $ K$ can be interchanged, since they are equivalent in the reciprocal space (see Section 3.5).
Subsections
previous up next   contents
 Previous: 3.3.3 Strain Resulting from Epitaxy   Up: 3. Strained Bulk Band Structure   Next: 3.4.1 Band Structure of Relaxed Si
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology