
Previous: 5.3.3 Coupling to the Schrödinger Poisson Solver Up: 5. Physical Mobility Modeling Next: 6. Simulation Results

5.4 MC Algorithm Including Degeneracy Effects

In transport calculations of the 2DEG forming in the channel of a MOSFET the inclusion of the Pauli principle is expected to be important since the lowest subband may lie well below the Fermi level even in the regime of moderate and high effective fields (high inversion layer concentrations). This leads to modified subband populations and an elevated mean kinetic energy of electrons as compared to the nondegenerate case. A change in the mobility is therefore to be expected.

Surprisingly, there is a discordance in the literature whether and how degeneracy effects should be included in transport calculations of inversion layers. Therefore, the ways to include the Pauli principle in a MC algorithm are revised and critically compared to each other. The usual method, where the Pauli blocking factor $[1-f({{\ensuremath{\mathitbf{k}}}})]$ is approximated using the equilibrium distribution function $f_{\mathrm{FD}}({{\ensuremath{\mathitbf{k}}}})$ , can be shown to lead to unphysical subband populations, kinetic energies, and mobilities. The reason being that at high degeneracy the error $\delta ({{\ensuremath{\mathitbf{k}}}}) = f({{\ensuremath{\mathitbf{k}}}}) - f_{\mathrm{FD}}({{\ensuremath{\mathitbf{k}}}})$ is dominant.

A new MC algorithm accounting for the Pauli exclusion principle is proposed which is less sensitive to the error $\delta ({{\ensuremath{\mathitbf{k}}}})$ . The proposed algorithm is based on the following reformulation of the collision operator

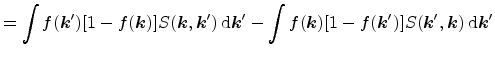$\displaystyle \mathcal{Q}[f]_{{{\ensuremath{\mathitbf{k}}}}}$	$\displaystyle = \int f({\ensuremath{\mathitbf{k}}}')[1-f({\ensuremath{\mathitbf... ...bf{k}}}',{\ensuremath{\mathitbf{k}}})\,\mathrm{d}{{\ensuremath{\mathitbf{k}}}'}$
	$\displaystyle = \int f({\ensuremath{\mathitbf{k}}}') S({\ensuremath{\mathitbf{k... ...)]}_{\mathrm{additional\,\, term}}\,\mathrm{d}{{\ensuremath{\mathitbf{k}}}'}\ ,$	(5.44)

where the band index

and the time dependence of the distribution are dropped. The last term represents a nonlinear correction to the nondegenerate collision operator. To linearize the scattering operator it is common to keep one factor of the product $f({\ensuremath{\mathitbf{k}}}) f({\ensuremath{\mathitbf{k}}}')$ constant and to treat the other as the unknown.

Near thermodynamic equilibrium, the distribution function can be approximated by the Fermi-Dirac distribution function $f_\mathrm{FD}$ . The key point of the new method is that a symmetric approximation with respect to ${{\ensuremath{\mathitbf{k}}}}$ and ${{\ensuremath{\mathitbf{k}}}'}$ is employed

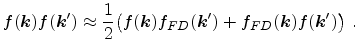$\displaystyle f({{\ensuremath{\mathitbf{k}}}}) f({{\ensuremath{\mathitbf{k}}}'}... ..._{FD}({{\ensuremath{\mathitbf{k}}}}) f({{\ensuremath{\mathitbf{k}}}'})\bigr)\ .$

(5.45)

Using this approximation the scattering operator can be expressed in terms of a modified transition rate $\widehat{S}({\ensuremath{\mathitbf{k}}},{\ensuremath{\mathitbf{k}}}')$ and scattering rate $\widehat{\lambda}_{{{\ensuremath{\mathitbf{k}}}}}$ as

$\displaystyle \mathcal{Q}[f]_{{{\ensuremath{\mathitbf{k}}}}} = \int f({{\ensure... ...suremath{\mathitbf{k}}}}) \widehat{\lambda}_{{{\ensuremath{\mathitbf{k}}}}}\ .$

with

$\displaystyle \widehat{S}({\ensuremath{\mathitbf{k}}}',{\ensuremath{\mathitbf{k}}})$	$\displaystyle = S({\ensuremath{\mathitbf{k}}}',{\ensuremath{\mathitbf{k}}})\lef... ...) \frac{1}{2}f_\mathrm{FD}({{\ensuremath{\mathitbf{k}}}'})\ , \quad\mathrm{and}$	(5.46)
$\displaystyle \widehat{\lambda}_{{{\ensuremath{\mathitbf{k}}}}}$	$\displaystyle = \int \widehat{S}({\ensuremath{\mathitbf{k}}}',{\ensuremath{\mathitbf{k}}}) \,\mathrm{d}{{\ensuremath{\mathitbf{k}}}'}\ .$	(5.47)

A simple error analysis shows the advantage of this formulation. Consider a highly degenerate state ${{\ensuremath{\mathitbf{k}}}}$ , characterized by $f({{\ensuremath{\mathitbf{k}}}}) \approx 1$ . A direct approximation of the blocking factor $[1-f({{\ensuremath{\mathitbf{k}}}})]$ can give completely wrong results, because the approximation of the blocking factor is determined by the error, $1-(f_{FD} + \delta) \approx \delta$ . In the formulation (5.46), however, because of $\delta \ll 1$ the effect of the error will be negligible, $1-(f_{FD} + \delta)/2 \approx 1/2$ .

The modified transition rate (5.46) is given by a linear combination of the forward rate $S({\ensuremath{\mathitbf{k}}},{\ensuremath{\mathitbf{k}}}')$ and backward rate $S({\ensuremath{\mathitbf{k}}}',{\ensuremath{\mathitbf{k}}})$ . The latter can be expressed in terms of the forward rate by means of the principle of detailed balance [Ashcroft76]. The modified scattering rates for phonon emission and absorption become,

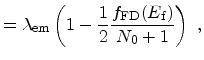$\displaystyle \widehat{\lambda}_\mathrm{em}$	$\displaystyle = \lambda_\mathrm{em} \left(1 - \frac{1}{2} \frac{f_{\mathrm{FD}}(E_\mathrm{f})}{N_0+1} \right)\ ,$	(5.48)
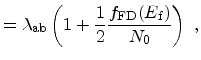$\displaystyle \widehat{\lambda}_\mathrm{ab}$	$\displaystyle = \lambda_\mathrm{ab} \left (1 + \frac{1}{2} \frac{f_\mathrm{FD}(E_\mathrm{f}) }{N_0} \right)\ ,$	(5.49)

where $E_\mathrm{f}$ denotes the final energy and

the equilibrium phonon distribution function,

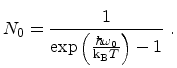
$\displaystyle N_0 = \frac{1}{\exp{\left (\frac{\hbar \omega_0}{\ensuremath {{\mathrm{k_B}}}T}\right )-1}}\ .$

To implement the Pauli principle in a conventional MC program for nondegenerate statistics the only modifications necessary are the replacement of the classical scattering rates by the modified ones.

For elastic scattering mechanisms the modified scattering rates do not change from the classical ones, $\widehat{\lambda}_{{{\ensuremath{\mathitbf{k}}}}} = \lambda_{{\ensuremath{\mathitbf{k}}}}$ . For the simulation of the 2DEG one can assume scattering with surface roughness, impurities, and acoustic phonons to be elastic.

In Section 6.3.2 simulation results using the new MC method including the Pauli exclusion principle are discussed. It is shown that in the low field limit the proposed algorithm yields the same mobility as the Kubo-Greenwood formula, while other algorithms do not. We use the new method to extract velocity profiles and to illustrate the large effect of degeneracy on the electron system.

Previous: 5.3.3 Coupling to the Schrödinger Poisson Solver Up: 5. Physical Mobility Modeling Next: 6. Simulation Results
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology