The hydrodynamic transport model is again obtained from the BTE by the
moment methods, however it accounts for the first three moments
instead of only two as the DD transport model. The resulting equations
are:
for electrons, where
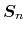 is the energy heat flux,
is the energy heat flux, 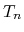 is
the electron temperature,
is
the electron temperature,
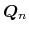 is the heat flow, and
is the heat flow, and
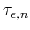 is the energy relaxation time of the electrons. The model is closed by
using Fourier's law for the heat term
is the energy relaxation time of the electrons. The model is closed by
using Fourier's law for the heat term
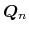 :
:
where
 is the thermal conductivity. The latter is calculated by the
Wiedemann-Franz law, proportional to the mobility
is the thermal conductivity. The latter is calculated by the
Wiedemann-Franz law, proportional to the mobility
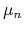 and carrier
temperature
and carrier
temperature 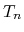 :
:
The factor 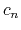 (
(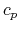 for holes, respectively) is set to zero so
that both terms of (4.18) have the same factor and any
inconsistency can be avoided. The model obtained is actually an energy
transport model as the moment equations were derived under the
assumption that the average kinetic energy of the carriers is
negligible in comparison to their thermal energy:
for holes, respectively) is set to zero so
that both terms of (4.18) have the same factor and any
inconsistency can be avoided. The model obtained is actually an energy
transport model as the moment equations were derived under the
assumption that the average kinetic energy of the carriers is
negligible in comparison to their thermal energy:
However, since in literature the terms energy transport and hydrodynamic transport are often used interchangeably, the name hydrodynamic transport is further retained.
S. Vitanov: Simulation of High Electron Mobility Transistors