Matrices arising from the discretization of differential operators are sparse,
because only neighbor points are considered. For that reason, only the non-zero
elements are stored in order to reduce the memory consumption (see the MCSR
format in Appendix E.1). However, during the factorization of the system
matrix
![]() into an upper and lower triangular matrix
into an upper and lower triangular matrix
![]() , additional matrix elements termed fill-in [193] become
non-zero. The profile
, additional matrix elements termed fill-in [193] become
non-zero. The profile
![]() is a measure for this fill-in
is a measure for this fill-in
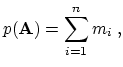 |
(4.22) |
| (4.23) |
and the bandwidth of the matrix is
![]() . Thus, the bandwidth of the
system matrix is the maximum distance between a diagonal and an off-diagonal
entry of the same row. Since storing of
. Thus, the bandwidth of the
system matrix is the maximum distance between a diagonal and an off-diagonal
entry of the same row. Since storing of
![]() requires additional
memory, a transformation is applied to reduce the bandwidth and the
profile. Thus, sorting algorithms sort the rows and columns of the system
matrix in such a way that the elimination performed by a Gaussian
type factorization yields a small number of fill-ins. The term
reordering can be used instead of sorting.
requires additional
memory, a transformation is applied to reduce the bandwidth and the
profile. Thus, sorting algorithms sort the rows and columns of the system
matrix in such a way that the elimination performed by a Gaussian
type factorization yields a small number of fill-ins. The term
reordering can be used instead of sorting.
The standard module provided by default obtains the sorting matrix
![]() (similar to
(similar to
![]() ) by a reverse Cuthill-McKee
algorithm [193,43]. It contains a single unity entry in each row
and is applied in such a way that rows and columns are equally swapped in order
to keep the diagonal dominance. In Figure 4.3 the reordered inner
system matrix with a significantly reduced bandwidth is shown. With
) by a reverse Cuthill-McKee
algorithm [193,43]. It contains a single unity entry in each row
and is applied in such a way that rows and columns are equally swapped in order
to keep the diagonal dominance. In Figure 4.3 the reordered inner
system matrix with a significantly reduced bandwidth is shown. With
![]() as the inner system and
as the inner system and
![]() equal
equal
![]() ,
sorting can be written as follows:
,
sorting can be written as follows:
The effort of the sorting algorithms as well as the effort for evaluating the
required storage (cf. symbolic phase) is
![]() each, with
each, with
![]() as the
numbers of non-zeros. By defining an average bandwidth
as the
numbers of non-zeros. By defining an average bandwidth
![]() as the average line length in the
as the average line length in the
![]() part or column
depth in the
part or column
depth in the
![]() part of the matrix, one can roughly estimate the space
consumption as
part of the matrix, one can roughly estimate the space
consumption as
![]() and the time consumption as
and the time consumption as
![]() [65].
[65].
As alternative to the in-house implementation of the reordering algorithm, external packages can be employed. For example, the Boost++ [27] (see Section 5.1.5) libraries provide a graph package with respective algorithms. In [193], the Gibbs-Poole-Stockmeyer algorithm [75] is suggested as an efficient alternative to the Cuthill-McKee-based algorithms. Further alternatives are the minimum degree [72] or nested dissection [71] algorithms.
In [44], a column approximate minimum degree ordering
algorithm is presented. Basically, sparse Gaussian
elimination with partial pivoting computes the factorization
![]() . While the row
ordering
. While the row
ordering
![]() is generated during factorization, the column ordering
is generated during factorization, the column ordering
![]() is used to limit the fill-in by considering the non-zero pattern in
is used to limit the fill-in by considering the non-zero pattern in
![]() . A
conventional minimum degree ordering requires the sparsity structure of
. A
conventional minimum degree ordering requires the sparsity structure of
![]() . Since the computation can be expensive,
alternative approaches are based on the sparsity structure of
. Since the computation can be expensive,
alternative approaches are based on the sparsity structure of
![]() instead.
instead.
In [183], an introduction is given to find unsymmetric permutations which try to maximize the elements on the diagonal of the matrix. Since matrices with zero diagonal entries cause problems for both direct and iterative solving techniques, the rows and columns are permuted in order that only non-zero elements remain on the diagonal only. Due to performance considerations and the applicable diagonal strategy during factorization (see Section 4.4), the assembly module does not provide such a feature. As a consequence, the simulator is obliged to avoid zero diagonal entries, which can be done in all cases of interest.