In general an MCSR or MCSC matrix is very well suited for sparse matrices with the diagonal elements all non-zero, which is a basic requirement for the in-house solver module (see Section 4.9). It consists of two parallel arrays of equal length but different data types. One array contains all indices (idx), the other all values (val).
The template MCSR class encapsulates all data members required for storing MCSR matrices and provides the interface to this data. The dimension of the system matrix is n. The number of non-zeros in the matrix is nnzall.
Note that all existing elements count as non-zero elements, even though their actual value might be zero. In context of Newton adjustment, it makes definitely sense to assembly also zero entries in order to reserve the space for elements which are later required. This can happen if transient contributions or ignored derivatives are later added.
The 
diagonal elements of the matrix are stored in the first
n array elements of the value array. The value of the 
-th
position val[i] is located in the -th row and -th column of
the square matrix. The off-diagonal elements are stored in the array positions
after the diagonal elements in the val array. In the case of a
MCSR matrix the off-diagonals are sorted by the row indices. All
off-diagonals of one row are stored sequentially. The
val array contains these sequences for all rows beginning with row
number 0. There is no space or separator between the sequences. The last
off-diagonal is stored at val[nnz].
The index array is required to store the column indices of the
respective values. This array runs in parallel to val.
First, the column numbers can be found in the positions
idx[n+1 ...nnz]. Second, the row numbers and the
border between two sequences/rows are needed. This information is
found in the lower part of the index array which runs in parallel to
the diagonal elements in the value array. For the -th row the begin
index of the sequence stored in the upper part is found at
idx[i]. Hence the end of the sequence equals the beginning
of the next row idx[i+1]. To enable a consistent treatment
of all rows, especially in loops, it is convenient to leave
val[n] unused, to keep the arrays parallel.
Using the MCSC format means that the off-diagonals are grouped by column. All off-diagonals of a column build up a sequence. Hence, the MCSC can be considered the transposed matrix stored in MCSR format.
As an example, the following
matrix should be stored in a MCSR structure
[228]:
First of all the four diagonal entries 2, 4, 6 and 8 are stored in the lower part of the value array - and then the four off-diagonals 1, 3, 5 and 7 in the upper part. nnz is eight, two arrays with a dimension of nine have to be allocated. The lower part of the value array contains the four diagonal entries, the next entry is left out and then the off-diagonals are stored sequentially. Hence, the value array looks like (u stands for unused):
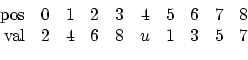
The lower part of the index array contains the starting index of every row in the upper part, the upper part the original column indices:
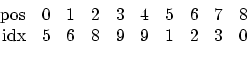
The access to this structure is straightforward. For instance, the entry at the position ([row,col]) [2, 2] should be derived. For a diagonal entry, the entry can be directly derived: val[2]=6. The next example is the off-diagonal [1, 3], hence the index array is needed. The off-diagonal sequence of row number 1 starts at position idx[1]=6. In case there are off-diagonal entries at all, their column indices have to compared with 3. So the number of off-diagonal entries of the first row is derived. The starting index of the sequence of the next row is idx[2]=8, hence there are two off-diagonals (idx[2]-idx[1]=8-6=2). The first one belongs to column idx[6]=2, so the next one has to be checked, idx[7]=3, which is the right position within the array. The last step is to read the value val[7]=5. If there is no value for an existing position stored, it is assumed to be zero.