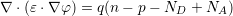
The basic semiconductor equations [1] consist of the Poisson equation (Equation 4.1),
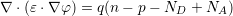 | (4.1) |
the continuity equations for electrons (Equation 4.2) and holes (Equation 4.3),
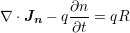 | (4.2) |
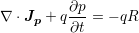 | (4.3) |
as well as the current relations for electrons (Equation 4.4) and holes (Equation 4.5)
 | (4.4) |
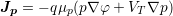 | (4.5) |
based on the DD model [103].
 denotes the permittivity,
denotes the permittivity, 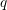 the elementary charge,
the elementary charge, 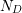 the donor doping
concentration, and
the donor doping
concentration, and 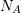 the acceptor doping concentration. With respect to the
continuity equations and the current relations,
the acceptor doping concentration. With respect to the
continuity equations and the current relations, 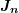 refers to the electron current
density,
refers to the electron current
density, 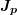 the hole current density,
the hole current density, 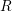 the recombination rate, and
the recombination rate, and 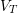 the thermal
voltage.
the thermal
voltage.
The DD model considers two charge transport mechanisms, those being charge carrier drift and diffusion, respectively. In general, charge carrier drift due to the presence of an electric field, implemented by the first term of the DD model, containing the gradient of the potential. On the contrary, diffusion is a fundamental process, which aims to establish a thermodynamic equilibrium in an initially imbalanced physical system. In the case of semiconductor physics, diffusion is achieved by carrier migration from areas with high concentration to areas where the concentration of particles is lower. Therefore, the DD model includes the second term, incorporating the gradient of the charge carrier concentration.
Substituting the current densities in the continuity equations (Equations 4.2-4.3) for the
current relations (Equations 4.4-4.5) yields a system of three partial differential equations
( PDEs), coupled via the potential 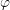 , the electron concentration
, the electron concentration  , and the hole
concentration
, and the hole
concentration 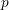 . These PDEs are typically discretized with the finite volume method to
conserve the current [1], stabilized by the Scharfetter-Gummel discretization [104], and
solved via nonlinear iterative solvers, such as the Newton scheme or the Gummel
method [1]. The solved potential, electron concentration, and hole concentration
distributions are used to compute, for instance, the current densities, essential to
evaluating the device performance via the current-voltage characteristics, where the
evaluated current at terminal contacts is related to the individually applied terminal
voltages.
. These PDEs are typically discretized with the finite volume method to
conserve the current [1], stabilized by the Scharfetter-Gummel discretization [104], and
solved via nonlinear iterative solvers, such as the Newton scheme or the Gummel
method [1]. The solved potential, electron concentration, and hole concentration
distributions are used to compute, for instance, the current densities, essential to
evaluating the device performance via the current-voltage characteristics, where the
evaluated current at terminal contacts is related to the individually applied terminal
voltages.
Although the basic semiconductor equations were successfully applied in the last decades, with the continuing shrinking of the device dimensions the typically applied DD model struggles to provide reasonable predictions [46]. Therefore, additional models have been developed [105], underlining the need for a modern device simulation software to support an exchangeable and expandable modeling backend.
As the focus of this work is on investigating approaches for a flexible device simulation framework, the actual transport model required for conducting device simulations is of marginal importance. Therefore, the simple yet representative DD transport model is sufficient for the subsequent investigations.
