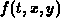 in the time dependent domain
in the time dependent domain 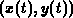 . Then, for the time derivative
. Then, for the time derivative 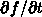 in
domain
in
domain 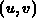 we get (3.3-56) from the chain rule.
we get (3.3-56) from the chain rule.




With moving grids the time derivatives must also be transformed. Assume a
time dependent function 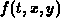 in the time dependent domain
in the time dependent domain 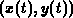 . Then, for the time derivative
. Then, for the time derivative 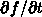 in
domain
in
domain 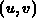 we get (3.3-56) from the chain rule.
we get (3.3-56) from the chain rule.
Here, the time derivative 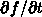 on the left side is at a
fixed position
on the left side is at a
fixed position 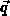 in the computational space, i.e. at a given grid
point. The time derivative
in the computational space, i.e. at a given grid
point. The time derivative 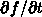 at the right side is at a
fixed position
at the right side is at a
fixed position 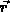 in the physical space, i.e. the
in the physical space, i.e. the 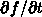 that appears in the governing physical equations. The quantity
that appears in the governing physical equations. The quantity
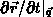 is the speed of the grid points.
The last term in (3.3-56) resembles a convective term and
accounts for the motion of the grid. Hereafter we will use
is the speed of the grid points.
The last term in (3.3-56) resembles a convective term and
accounts for the motion of the grid. Hereafter we will use 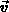 for the
speed of the grid points.
for the
speed of the grid points.
With the time derivatives transformed, only time derivatives at fixed points in the computational domain will appear in the equations. Therefore, all computations can be done on the fixed grid in the domain without interpolation even though the grid points are in motion in the physical space.
The expression (3.3-56) for the transformation of the time
derivatives was obtained by a chain rule expansion. To get a conservative
form for the transformed time derivatives we apply the divergence theorem to
an area element 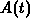 at time
at time 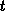 and to the same element at time
and to the same element at time
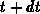 ,
, 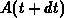 . Then making up a balance equation and proceeding to the
limit
. Then making up a balance equation and proceeding to the
limit 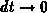 , we obtain (3.3-57).
, we obtain (3.3-57).
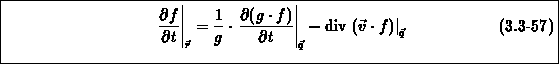
The structure of (3.3-57) is easily grasped. Since 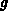 is a
measure for the area, the first term
is a
measure for the area, the first term 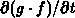 covers
the change of the amount of quantity
covers
the change of the amount of quantity 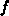 within a cell, whereas the second
term covers the flux
within a cell, whereas the second
term covers the flux 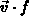 through the moving cell boundaries.
through the moving cell boundaries.
Again, it is straightforward to proof that (3.3-56) and (3.3-57) are mathematically identical.



