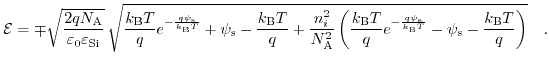Next: E. Flatband Potential and
Up: Appendix
Previous: C. Estimating Diffusive Layer
D. Relation Between Charge Density and Potential Drop in the MOSFET Channel
The relation between the charge density in the MOSFET channel and the potential drop (assuming an n-channel MOS transistor) can be obtained from the Poisson equation using the prerequisite of the validity of Boltzmann distributed electrons and holes. Interrestingly, this leads to an equation very similar to the Poisson-Boltzmann model of the electrolyte:
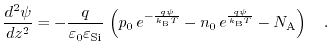 |
(7.29) |
Since, the overall charge has to be zero,
 must be fullfilled.
Substituting
must be fullfilled.
Substituting
 by the relation before the following expression is derived:
by the relation before the following expression is derived:
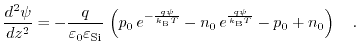 |
(7.30) |
Now, grouping the expressions containing 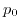 and
and 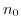 :
:
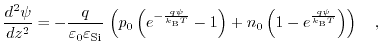 |
(7.31) |
followed by the relation
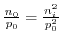 and the assumption that
and the assumption that
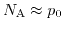 , (p-doped), we get:
, (p-doped), we get:
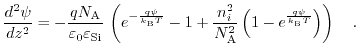 |
(7.32) |
The equation connecting the potential and the doping can now be deduced.
The identity:
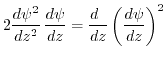 |
(7.33) |
is introduced in order to rewrite (7.32) as a differential equation of first order:
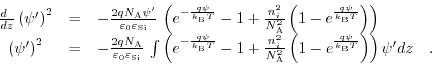 |
(7.34) |
The boundary conditions are set to 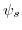 at the surface, and 0 for
at the surface, and 0 for
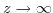 :
:
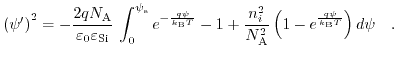 |
(7.35) |
After the integration the following relation is gained:
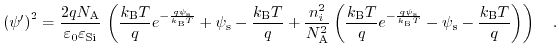 |
(7.36) |
Since the electric field is related to the potential via
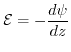 , the derived expression describes the dependence of the electric field on the surface potential:
, the derived expression describes the dependence of the electric field on the surface potential:
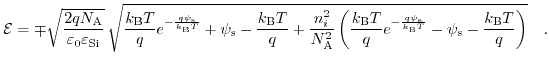 |
(7.37) |
Applying Gauß's law:
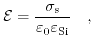 |
(7.38) |
leads to the desired formultaion, connecting the surface charge density
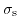 with the surface potential
with the surface potential
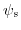 :
:
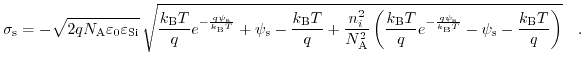 |
(7.39) |




Next: E. Flatband Potential and
Up: Appendix
Previous: C. Estimating Diffusive Layer
T. Windbacher: Engineering Gate Stacks for Field-Effect Transistors
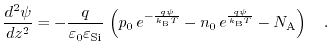
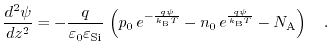
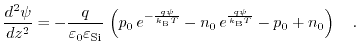
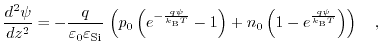
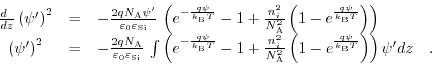
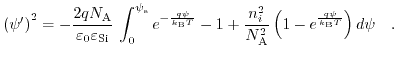
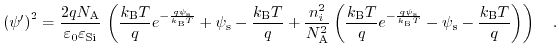
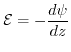 , the derived expression describes the dependence of the electric field on the surface potential:
, the derived expression describes the dependence of the electric field on the surface potential: