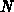 points in
points in
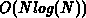 time [Prep85][Hala94]. According to the EULER
formula, such a triangulation of a vertex set
time [Prep85][Hala94]. According to the EULER
formula, such a triangulation of a vertex set 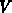 has at most
has at most 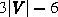 edges.
edges.




The KIRKPATRICK point location method is also termed triangulation refinement method for point location [Kirk83][Prep85], because it is based on a hierarchy of triangulations. The initial grid makes up the lowest (finest) level of the hierarchy, and the upper levels are constructed as coarsened triangulations of the next lower level.
A precondition for applying the KIRKPATRICK method is that the lowest
level has to be a triangulation. This is not always the case, but there exist
algorithms to triangulate any given point set consisting of 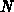 points in
points in
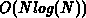 time [Prep85][Hala94]. According to the EULER
formula, such a triangulation of a vertex set
time [Prep85][Hala94]. According to the EULER
formula, such a triangulation of a vertex set 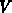 has at most
has at most 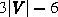 edges.
edges.
Surrounding the initial grid, a bounding triangle is assumed where the initial
triangulation is inscribed. This has the effect that the top level
triangulation consists of only this one triangle. 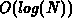 locate time is
only guaranteed with this precondition.
locate time is
only guaranteed with this precondition.
Let the grid hierarchy be a sequence of triangulations 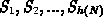 , where
, where 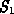 is the initial
is the initial 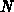 -vertex triangulation
-vertex triangulation 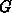 . The
method to obtain the triangulation
. The
method to obtain the triangulation 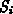 from
from 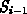 is shown in
Algorithm 7.1.
is shown in
Algorithm 7.1.
This sequence of triangulations is now stored as a search-directed acyclic graph (SDAG), which is a tree structure whose nodes are triangles. Fig. 7.9 shows how a triangulation is coarsened through vertex removal, and Fig. 7.10 shows the corresponding SDAG.
Figure: Coarsening the initial triangulation through point removal.
Case (a) shows an initial triangulation consisting of 9 rectangles which is
coarsened in four steps. Points with a degree of less than five (constant  is chosen to be five) are marked for removal and shown encircled. Note that in
case (b) boundary points lying on a straight line are selected.
is chosen to be five) are marked for removal and shown encircled. Note that in
case (b) boundary points lying on a straight line are selected.
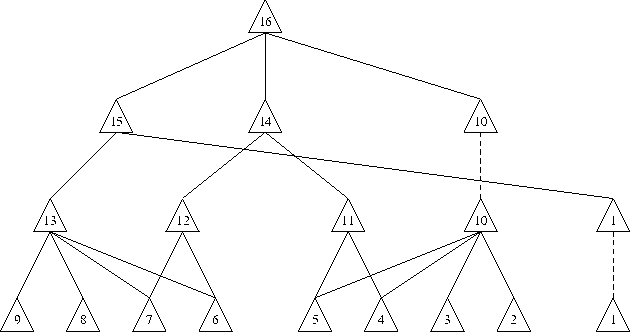
Figure: The resulting search-directed acyclic graph. Solid lines denote direct
references. Dashed lines denote promotion of nodes. Since 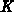 was chosen to be
five, at most four nodes are referenced by inner nodes.
was chosen to be
five, at most four nodes are referenced by inner nodes.
In this implementation of the KIRKPATRICK point location method, three deviations from Algorithm 7.1 are made:
Multiply connected regions in two dimensions are handled correctly, because if no surrounding triangle is generated, the top-level grid always matches exactly the geometry. Only in the case of a surrounding triangle, inner nodes would be generated which refer to ``void'' triangles, i.e. triangles not included in the initial geometry. If a point location would encounter such a void triangle, the point is not included in the initial grid and the location process is done.
Point location in the SDAG now proceeds according to
Algorithm 7.2. Initially, the questioned point 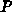 is tested for
inclusion in the triangulation
is tested for
inclusion in the triangulation 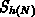 . The test for inclusion in a
triangle to be used throughout the location process can be carried out in
. The test for inclusion in a
triangle to be used throughout the location process can be carried out in
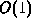 time
time . If the point is
included in the root triangle, then it is tested for inclusion in one of its
descendants. This process is repeated until a triangle belonging to
. If the point is
included in the root triangle, then it is tested for inclusion in one of its
descendants. This process is repeated until a triangle belonging to 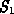 is
reached.
is
reached.



