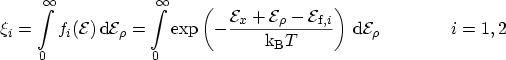For non-degenerate semiconductors the FERMI energy is located below the
conduction band edge. Therefore,
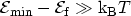 holds in expression
(3.13) and the FERMI-DIRAC distribution (3.15) can be
approximated by a MAXWELL-BOLTZMANN (or MAXWELLian) distribution
holds in expression
(3.13) and the FERMI-DIRAC distribution (3.15) can be
approximated by a MAXWELL-BOLTZMANN (or MAXWELLian) distribution
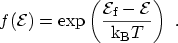 |
(3.20) |
This expression is compared to the FERMI-DIRAC distribution in
Fig. 3.3. It can be seen that only for energies well above the
FERMI energy the expressions deliver equal results.
Figure 3.3:
Comparison of the FERMI-DIRAC and the
MAXWELL-BOLTZMANN distribution on a linear scale (left) and on a logarithmic
scale (right). At energies above the FERMI energy the expressions yield
similar results.
|
|
Using this expression, 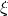 in (3.14) becomes
in (3.14) becomes
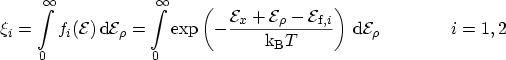 |
(3.21) |
which evaluates to
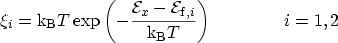 |
(3.22) |
and yields a supply function of
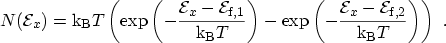 |
(3.23) |
A. Gehring: Simulation of Tunneling in Semiconductor Devices
![\includegraphics[width=.49\linewidth]{figures/fermiMaxwell}](img313.png)
![\includegraphics[width=.49\linewidth]{figures/fermiMaxwellLog}](img314.png)
![]() in (3.14) becomes
in (3.14) becomes