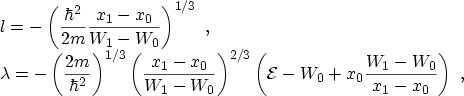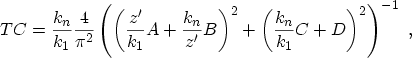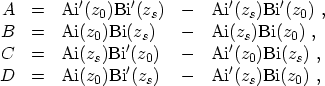3.5.2 The GUNDLACH Method
The GUNDLACH method [137] provides an analytical solution of
SCHRÖDINGER's equation for a linear energy barrier. The one-dimensional
time-independent SCHRÖDINGER equation in this case reads
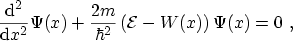 |
(3.61) |
with the linear potential energy 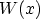 between the points
between the points 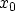 and
and 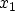 ,
,
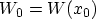 , and
, and
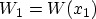 ,
,
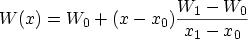 |
(3.62) |
for
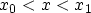 . Using the abbreviations
. Using the abbreviations
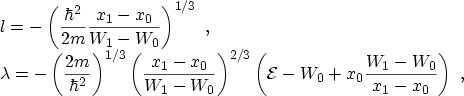 |
(3.63) |
and
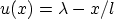 , expression (3.61) turns into
, expression (3.61) turns into
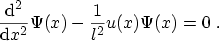 |
(3.64) |
With
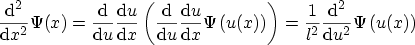 |
(3.65) |
SCHRÖDINGER's equation evolves into the AIRY3.7 differential equation
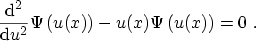 |
(3.66) |
The solutions of this differential equation are the AIRY functions
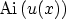 and
and
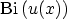 [138], which are depicted in
Fig. 3.10 together with their derivatives. The wave functions
consist of linear superpositions of these AIRY functions
[138], which are depicted in
Fig. 3.10 together with their derivatives. The wave functions
consist of linear superpositions of these AIRY functions
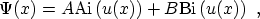 |
(3.67) |
where the function  is given as
is given as
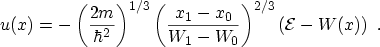 |
(3.68) |
Figure 3.10:
The AIRY functions Ai and Bi and their
derivatives.
|
|
Assuming a constant electron mass in the dielectric, GUNDLACH derives an
expression for the transmission coefficient
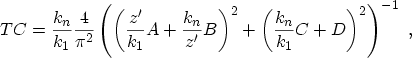 |
(3.69) |
where the abbreviations
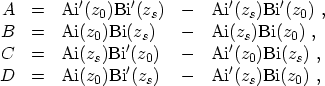 |
(3.70) |
have been used and the symbols 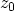 ,
, 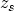 , and
, and 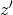 are given by
are given by
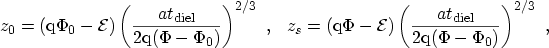 |
(3.71) |
and
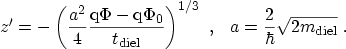 |
(3.72) |
The symbols
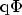 and
and
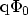 denote the two edges of the energy barrier
as shown in Fig. 3.9. The GUNDLACH method is frequently used in the
literature [121,139] and implemented in device
simulators. Numerical problems may occur for flat barriers (
denote the two edges of the energy barrier
as shown in Fig. 3.9. The GUNDLACH method is frequently used in the
literature [121,139] and implemented in device
simulators. Numerical problems may occur for flat barriers (
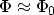 ) due to the exponential increase of the AIRY functions
) due to the exponential increase of the AIRY functions
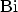 and
and
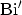 for positive arguments. In practical implementations the values of
for positive arguments. In practical implementations the values of
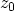 and
and 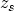 have been bounded to values below
have been bounded to values below
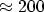 to avoid
floating point overflow.
to avoid
floating point overflow.
A. Gehring: Simulation of Tunneling in Semiconductor Devices