|
|
|
|
Previous: 3.8.2 The Model of JIMÉNEZ et al. Up: 3.8.2 The Model of JIMÉNEZ et al. Next: 3.8.2.2 Capture and Emission Times |
The tunneling model is based on a two-step tunneling process via traps in the dielectric which incorporates energy loss by phonon emission [219]. Fig. 3.17 shows the basic two-step process of an electron tunneling from a region with higher FERMI energy (the cathode) to a region with lower FERMI energy (the anode). To avoid integration in energy, the initial electron energy is assumed to be located at the average kinetic energy, which, for the parabolic dispersion relation (3.1) and the MAXWELLian distribution (3.20), is
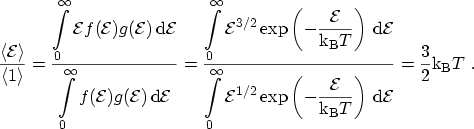 |
(3.130) |
The rate with which an electron with energy
![]() is captured by a trap
located at position
is captured by a trap
located at position ![]() and energy
and energy
![]() is given by [221]
is given by [221]
The population of phonons
![]() is given by the
BOSE3.11-EINSTEIN3.12 statistics
is given by the
BOSE3.11-EINSTEIN3.12 statistics
| (3.132) |
The function ![]() is the modified BESSEL3.13 function of order
is the modified BESSEL3.13 function of order ![]() , with
, with
| (3.133) |
| (3.135) |
The numerical evaluation of (3.134) requires the calculation of the wave functions in the dielectric layer, which, however, degrades the computational efficiency of a multi-purpose device simulator where simulation speed is crucial. To avoid this, the barriers have been transformed to take advantage of the well known solutions for constant potentials. Two cases must be distinguished, namely the case of a trapezoidal barrier and the case of a triangular barrier. The two cases are depicted in Fig. 3.18.
![\includegraphics[width=0.48\linewidth]{figures/wave2}](img643.png)
![\includegraphics[width=0.48\linewidth]{figures/wave}](img644.png)
|
For capture processes and for emission processes where the electron faces a
trapezoidal barrier, the barrier is transformed into a step function of
height equal to the potential at the middle point between ![]() and
and
![]() (
(
![]() in the left part of Fig. 3.18),
in the left part of Fig. 3.18), ![]() being the
position of the trap inside the dielectric. Assuming
being the
position of the trap inside the dielectric. Assuming
| (3.136) |
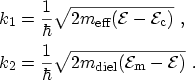 |
(3.138) |
For emission processes in which the barrier is triangular (the electron
energy is above the dielectric conduction band at some point between the trap
and the anode), two regions in the dielectric must be distinguished. The first
one, between the interface at ![]() and the point
and the point
![]() (see the right part
of Fig. 3.18) has the height
(see the right part
of Fig. 3.18) has the height
![]() . The height of the
approximated barrier in the other region is then the value of the barrier,
. The height of the
approximated barrier in the other region is then the value of the barrier,
![]() , in the middle point between
, in the middle point between
![]() and the position of the trap
and the position of the trap
![]() . With this new barrier and the assumptions for the wave functions in
the three regions
. With this new barrier and the assumptions for the wave functions in
the three regions
| (3.139) | |||
| (3.140) | |||
| (3.141) |
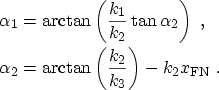 |
(3.143) |
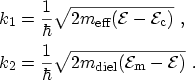 |
(3.144) |
A. Gehring: Simulation of Tunneling in Semiconductor Devices