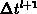 the following quantities related to the interface traps
the following quantities related to the interface traps 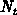 at the level
at the level 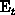 should be calculated during each iteration
should be calculated during each iteration 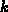 :
:




Considering the solution of the complete system of equations for the time step
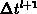 the following quantities related to the interface traps
the following quantities related to the interface traps 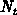 at the level
at the level 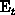 should be calculated during each iteration
should be calculated during each iteration 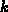 :
:
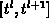 to obtain the actual trap occupancy
function at the end of the interval
to obtain the actual trap occupancy
function at the end of the interval
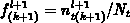 . The occupancy function at the
previous time step
. The occupancy function at the
previous time step 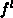 is known from the selfconsistent solution of
the complete system of equations.
is known from the selfconsistent solution of
the complete system of equations.
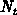
where 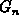 ,
, 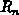 ,
, 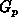 and
and 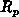 are given by
relationships 3.4 and 3.5. For the
non-interacting traps the relationship
are given by
relationships 3.4 and 3.5. For the
non-interacting traps the relationship
holds in general. In addition, the derivatives with respect to
concentrations
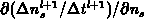 and
and
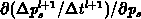 are calculated.
are calculated.
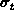 with respect to surface potential
with respect to surface potential
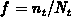 , assuming non-interacting traps, reads (we omit the iteration
counter
, assuming non-interacting traps, reads (we omit the iteration
counter 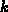 hence):
hence):
This is a first order linear differential equation, with non-constant
coefficients. The analytical solution to 3.34 in the interval
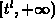 is
is
where we used the initial condition 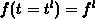 . The effective time constant
. The effective time constant
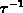 has the form
has the form 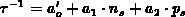 , while
, while
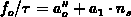 , where
, where 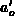 ,
, 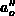 ,
, 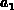 and
and 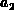 are
constant assuming that the trap energy and capture cross-sections are constant.
For the non-steady-state emission and the capture when the free-carrier
concentrations at the surface are constant in the interval
are
constant assuming that the trap energy and capture cross-sections are constant.
For the non-steady-state emission and the capture when the free-carrier
concentrations at the surface are constant in the interval 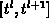 , the
factors
, the
factors  and
and 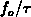 are constant. The general
solution 3.35 then reduces to a simple analytical form:
are constant. The general
solution 3.35 then reduces to a simple analytical form:
When the surface carrier concentrations vary during the time step
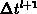 , the integral in 3.35 has no analytical
solution in the general case. Since the basic semiconductor equations are solved
at
, the integral in 3.35 has no analytical
solution in the general case. Since the basic semiconductor equations are solved
at 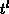 and
and 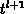 only, we have no information on
only, we have no information on 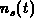 and
and 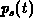 in the integration interval. Assuming a physics based exponential interpolation
of
in the integration interval. Assuming a physics based exponential interpolation
of 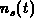 and
and 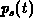 as discussed later, no analytical solution
is available in 3.35
as discussed later, no analytical solution
is available in 3.35 . To overcome this problem,
we will apply a pure numerical approach to solve the differential
equation 3.34. Using the strongly implicit discretization
of 3.34 it follows that the solution at
. To overcome this problem,
we will apply a pure numerical approach to solve the differential
equation 3.34. Using the strongly implicit discretization
of 3.34 it follows that the solution at 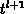 yields
yields
where  and
and 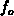 are calculated for the point
are calculated for the point 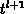 . The time interval
. The time interval
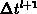 in 3.37 does not necessarily denote the time
step for solving the basic semiconductor equations. In fact, we can divide
in 3.37 does not necessarily denote the time
step for solving the basic semiconductor equations. In fact, we can divide
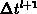 into several subintervals and apply the
solution 3.37 to each of them, as we shall explain later. The
solution 3.37 exhibits proper limiting behaviors:
into several subintervals and apply the
solution 3.37 to each of them, as we shall explain later. The
solution 3.37 exhibits proper limiting behaviors:
This solution, however, deviates from the exact solution to the problem when it
is known, as for the important cases described by 3.36. For this
`natural solution' the time discretization error of 3.37 is
analyzed in detail in Appendix B. By analytical considerations it
is found that a quite small number of time steps within the interval of the gate
pulse which determines the emission mode, are sufficient to suppress the
discretization error.
To calculate the net generation rates 3.29, let us remark
that replacing 3.4 and 3.5 in 3.29,
and using 3.30 leads to
where 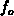 and
and  are constant in the interval of integration.
It follows
are constant in the interval of integration.
It follows
respectively. Note that 3.40 and 3.41 directly
follow from 3.29 by simply replacing all subintegral quantities
with their values at 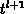 .
.
The corresponding derivation of the generation rates in the interval
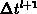 , with respect to the carrier concentrations become
, with respect to the carrier concentrations become
For the derivation of the trapped charge with respect to the surface potential 3.33 we obtain
In the derivation of 3.42 - 3.44,
Maxwell-Boltzmann statistics and constant capture cross-sections are assumed.
Note that we employ the derivations to accelerate convergence only.
In the limit 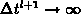 the
expressions 3.40 - 3.44 are reduced properly to
the steady-state relationships; e.g. the
expressions 3.40 and 3.41 reduce to the
well-known Shockley-Read-Hall trap-assisted recombination rate model for the
steady-state [409][179].
the
expressions 3.40 - 3.44 are reduced properly to
the steady-state relationships; e.g. the
expressions 3.40 and 3.41 reduce to the
well-known Shockley-Read-Hall trap-assisted recombination rate model for the
steady-state [409][179].
In the consideration above we solve the differential
equation 3.34 numerically in one step. Dividing 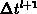 into several subintervals and interpolating
into several subintervals and interpolating 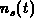 and
and 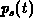 between
between
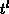 and
and 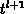 , allows us to solve equation 3.34 with a
higher accuracy than by the one-step method. To propose a convenient
interpolation for the carrier concentrations, we remember that large variations
of
, allows us to solve equation 3.34 with a
higher accuracy than by the one-step method. To propose a convenient
interpolation for the carrier concentrations, we remember that large variations
of 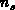 and
and 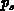 take place when the variations of the surface potential are
large. This occurs in weak inversion, depletion and weak accumulation.
The surface potential almost linearly follows the gate voltage in these regions
(see expression B.11 in Appendix B), which produces
exponential variations of the surface concentrations. Therefore, an exponential
interpolation of
take place when the variations of the surface potential are
large. This occurs in weak inversion, depletion and weak accumulation.
The surface potential almost linearly follows the gate voltage in these regions
(see expression B.11 in Appendix B), which produces
exponential variations of the surface concentrations. Therefore, an exponential
interpolation of 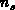 and
and 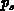 between two time steps of the gate bias is
assumed. On the other hand, in the regions where the surface potential varies
logarithmically (strong inversion and accumulation), variations of the
surface carrier concentrations are small and the time discretization error
becomes small as well.
between two time steps of the gate bias is
assumed. On the other hand, in the regions where the surface potential varies
logarithmically (strong inversion and accumulation), variations of the
surface carrier concentrations are small and the time discretization error
becomes small as well.
In each time subinterval the strongly implicit discretization is applied,
leading to a recursive expression of form 3.37. Beginning
from 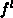 the occupancy function can be easily calculated at the
discretization points, until the last value
the occupancy function can be easily calculated at the
discretization points, until the last value 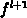 . The dependence of the
time discretization error in the numerical approach 3.37 on
the time steps in the gate bias and the number of time-subintervals
is analyzed in detail in Appendix B. Evidently, by dividing
. The dependence of the
time discretization error in the numerical approach 3.37 on
the time steps in the gate bias and the number of time-subintervals
is analyzed in detail in Appendix B. Evidently, by dividing
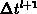 into
into  subintervals, the gate bias steps
subintervals, the gate bias steps 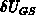 are reduced effectively to
are reduced effectively to 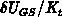 with respect to the
trap-dynamics equations.
with respect to the
trap-dynamics equations.
The expressions for the net generation rates in the particular subinterval are
given by expressions 3.40 and 3.41 divided by
the number of the subintervals, but with all quantities replaced with their
values at the end of the subinterval. The total net generation rate within
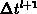 becomes the sum of the particular contributions from each
subinterval. The expressions for the derivatives are evaluated by recursion,
as well. They are quite clumsy and will be omitted here.
becomes the sum of the particular contributions from each
subinterval. The expressions for the derivatives are evaluated by recursion,
as well. They are quite clumsy and will be omitted here.
A similar exponential interpolation of 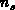 and
and 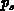 can be performed
between adjacent grid lines along the interface. This interpolation is
important for interface traps in the junctions, since the free carrier
concentrations vary rapidly with the position in these regions.
can be performed
between adjacent grid lines along the interface. This interpolation is
important for interface traps in the junctions, since the free carrier
concentrations vary rapidly with the position in these regions.
A comment will be made on the computer implementation of the previous
relationships. If the complementary occupancy function is calculated
from 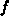 as
as 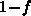 , its minimal value is limited by the accuracy of
, its minimal value is limited by the accuracy of 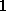 , but
not by the minimal positive real number representable in the computer. Since
this truncation can include an error in the expressions presented, the
complementary occupancy function should be calculated by
, but
not by the minimal positive real number representable in the computer. Since
this truncation can include an error in the expressions presented, the
complementary occupancy function should be calculated by
where 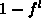 is the complementary occupancy function known from the previous
time step and
is the complementary occupancy function known from the previous
time step and 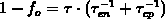 .
.
An equidistant discretization in the energy space has been assumed for a
continuum of interface states, with the spacing of 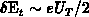 between two adjacent energy levels
between two adjacent energy levels . By this choice
the equilibrium Fermi-Dirac occupancy function (3.8) is resolved
well. Additionally, for the non-steady-state emission occupancy function
(B.5) about
. By this choice
the equilibrium Fermi-Dirac occupancy function (3.8) is resolved
well. Additionally, for the non-steady-state emission occupancy function
(B.5) about 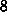 trap levels contribute effectively to the signal
in each time decade (see Figure B.1). The number of energy levels
becomes
trap levels contribute effectively to the signal
in each time decade (see Figure B.1). The number of energy levels
becomes 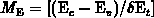 . Note that
. Note that
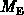 is temperature dependent: e.g. at room temperature
is temperature dependent: e.g. at room temperature 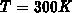 ,
,
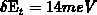 and
and 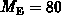 , while at
, while at 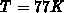 ,
,
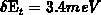 and
and 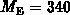 .
.
To calculate the total contribution from traps at 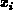 , the contributions
from all energy levels
, the contributions
from all energy levels 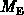 are superposed. The total electron and hole
net generation rates, the total trapped charge and their
derivatives at
are superposed. The total electron and hole
net generation rates, the total trapped charge and their
derivatives at 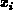 become sums of the contributions from the particular
levels.
They are coupled with the basic semiconductor equations through the terms
become sums of the contributions from the particular
levels.
They are coupled with the basic semiconductor equations through the terms
 ,
, 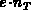 and their derivatives (see
equations 3.26 and 3.28). The complete system
is solved selfconsistently at each time step. The detailed algorithm is
presented in Appendix C. The derivatives of the generation rates
with respect to the carrier concentrations are used to improve the convergence
of the discretized continuity equations 3.26, while the
derivatives of the trapped charge accelerates the convergence of the discretized
Poisson equation 3.28. Moreover, the last is absolutely
indispensible in achieving the convergence of the iterative algorithm when high
trap-densities are assumed. After extensive numerical tests, the
convergence of the algorithm could be guaranteed, for both steady-state and
transient conditions and both donor-like and acceptor-like interface
traps, for densities
and their derivatives (see
equations 3.26 and 3.28). The complete system
is solved selfconsistently at each time step. The detailed algorithm is
presented in Appendix C. The derivatives of the generation rates
with respect to the carrier concentrations are used to improve the convergence
of the discretized continuity equations 3.26, while the
derivatives of the trapped charge accelerates the convergence of the discretized
Poisson equation 3.28. Moreover, the last is absolutely
indispensible in achieving the convergence of the iterative algorithm when high
trap-densities are assumed. After extensive numerical tests, the
convergence of the algorithm could be guaranteed, for both steady-state and
transient conditions and both donor-like and acceptor-like interface
traps, for densities 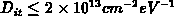 of traps
very localized in space and
of traps
very localized in space and 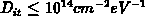 for traps
uniformly distributed in space. These limits are much higher than the
densities of interest in practice. Assuming bulk traps the empirical limit
becomes
for traps
uniformly distributed in space. These limits are much higher than the
densities of interest in practice. Assuming bulk traps the empirical limit
becomes 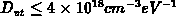 for traps nonlocalized in
space.
for traps nonlocalized in
space.



