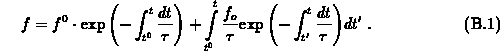




Discretization Error in the Trap Equation: An Analysis
An analytical evaluation of the error is done for a special, but in practice very important, case. The general solution of the trap-dynamics equation is given by
Assuming non-steady-state emission the general solution reduces to
For simplicity, but without loss in generality, we assume for the initial
condition 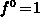 at
at 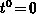 and for the steady-state occupancy
function
and for the steady-state occupancy
function 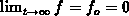 , for traps of interest. Also,
, for traps of interest. Also,
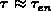 holds. Let us consider the condition at the interface
at the specific time
holds. Let us consider the condition at the interface
at the specific time 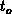 . The occupancy function becomes
. The occupancy function becomes
In practice, 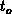 is some characteristic time in the measurement signal, as
the emission time determined by the rise or fall times of the gate pulse in
Figure 3.2, the emission time which equals to
is some characteristic time in the measurement signal, as
the emission time determined by the rise or fall times of the gate pulse in
Figure 3.2, the emission time which equals to 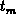 in
Figure 3.3, or the time constants which define the emission
window in the DLTS techniques. This time corresponds to an energy level
in
Figure 3.3, or the time constants which define the emission
window in the DLTS techniques. This time corresponds to an energy level
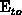 so that
so that 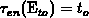 holds.
It follows
holds.
It follows
Let  denotes the normalized relative trap energy with respect to the level
denotes the normalized relative trap energy with respect to the level
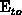 :
: 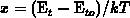 . Solution B.3 reduces to
. Solution B.3 reduces to
Note that 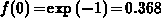 . Expression B.5 represents
the exact solution for the occupancy function at
. Expression B.5 represents
the exact solution for the occupancy function at 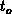 in the non-steady-state
emission mode. This universal function is graphically presented by solid line
in Figure B.1.
in the non-steady-state
emission mode. This universal function is graphically presented by solid line
in Figure B.1.
Let us consider the numerical solution to the non-steady-state emission problem,
which is obtained by using the strongly implicit discretization. We assume an
equidistant discretization in time for simplicity:
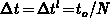 ,
, 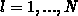 . The
. The 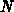 is the number of
time subintervals in
is the number of
time subintervals in 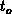 . The solutions in the individual intervals become
. The solutions in the individual intervals become
Note that 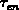 remains constant in time. Remember that
remains constant in time. Remember that 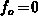 and
and
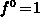 are assumed at the beginning of our analysis. It is easy to derive
the numerical solution
are assumed at the beginning of our analysis. It is easy to derive
the numerical solution 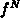 at
at 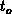
Using 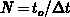 and
and 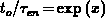 with
with
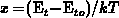 , the numerical solution using the
strongly implicit discretization becomes
, the numerical solution using the
strongly implicit discretization becomes
Comparing B.8 with B.5 one is able to determine the
number of discretization intervals 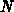 necessary to obtain the numerical
solution with the desired accuracy. It is evident:
necessary to obtain the numerical
solution with the desired accuracy. It is evident:
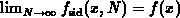 . The solution
. The solution 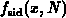 is compared with
is compared with 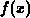 in Figure B.1 (left), with
in Figure B.1 (left), with
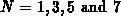 as parameter. Figure B.1 (right) shows
an absolute error in the numerically calculated occupancy function versus the
relative trap energy. For
as parameter. Figure B.1 (right) shows
an absolute error in the numerically calculated occupancy function versus the
relative trap energy. For 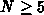 the absolute error in the trap occupancy lies
below
the absolute error in the trap occupancy lies
below 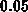 . Consequently, in order to keep the time discretization error
acceptably small the time intervals in the terminal pulses which govern the
emission modes must be resolved by more than
. Consequently, in order to keep the time discretization error
acceptably small the time intervals in the terminal pulses which govern the
emission modes must be resolved by more than 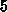 time steps in our numerical
simulation.
time steps in our numerical
simulation.
The previous analysis is done for the non-steady-state emission. It is valid
for the capture as well, assuming that the free-carrier concentration at the
interface is constant in time. For the capture with non-constant free carrier
concentrations (as during the rising or falling edges of the gate pulse or when
the charge-potential-feedback effect takes place) or when both, the capture and
the emission influence the trap level simultaneously, the coefficients  and
and 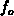 in 3.10 change in time in a complex manner. In these
cases, solution B.1 cannot be reduced to an analytical form.
However, the exact solution can always be obtained numerically, applying
sufficiently fine time steps. Figure B.2 shows the evolution
of the occupancy function during the rising edge of the gate pulse for three
characteristic traps. The gate voltage rises from strong accumulation
(
in 3.10 change in time in a complex manner. In these
cases, solution B.1 cannot be reduced to an analytical form.
However, the exact solution can always be obtained numerically, applying
sufficiently fine time steps. Figure B.2 shows the evolution
of the occupancy function during the rising edge of the gate pulse for three
characteristic traps. The gate voltage rises from strong accumulation
(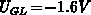 ) to weak inversion (
) to weak inversion (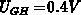 ) in
) in 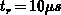 .
After the rising edge, the interval
.
After the rising edge, the interval 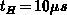 follows. The traps at the
level
follows. The traps at the
level 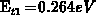 are filled, at first by the hole emission and
later by the electron capture. The traps at
are filled, at first by the hole emission and
later by the electron capture. The traps at 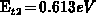 , chosen
in the midgap region, are filled by the electron capture only. For the level
, chosen
in the midgap region, are filled by the electron capture only. For the level
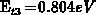 both processes, the electron capture and the electron
emission take place with comparable time constants.
both processes, the electron capture and the electron
emission take place with comparable time constants.
The numerical result given in Figure B.2 is obtained by the
strongly implicit discretization of the trap-dynamics equation, but without
dividing the time steps (says 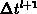 ) into
) into  subintervals
(
subintervals
(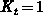 ). In fact, we discuss the worst case, when the trap-dynamics
equations are discretized in time as the basic semiconductor equations.
). In fact, we discuss the worst case, when the trap-dynamics
equations are discretized in time as the basic semiconductor equations.
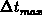 is the characteristic time interval in the time stepping method
we implemented
is the characteristic time interval in the time stepping method
we implemented . Because of
. Because of 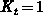 , roughly speaking
, roughly speaking 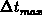 corresponds to
corresponds to 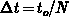 in the previous analytical consideration.
The population of
in the previous analytical consideration.
The population of 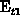 is well reproduced when
is well reproduced when
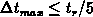 . For the electron capture by traps
. For the electron capture by traps 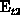 and
and 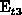 , the trap occupancy is overestimated at the onset of the
capture (close to
, the trap occupancy is overestimated at the onset of the
capture (close to 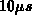 ). This discretization error occurs because
). This discretization error occurs because 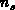 is
evaluated at the end of the interval
is
evaluated at the end of the interval 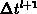 . At the rising edge of the
gate pulse, however, the electron concentration varies
significantly
. At the rising edge of the
gate pulse, however, the electron concentration varies
significantly . Therefore, an average
. Therefore, an average 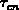 is quite
underestimated in the interval
is quite
underestimated in the interval 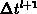 . Decreasing
. Decreasing 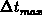 the
variation of
the
variation of 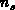 in the discretization interval and, consequently, the
discretization error are reduced (Figure B.2).
in the discretization interval and, consequently, the
discretization error are reduced (Figure B.2).
By dividing 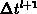 into
into 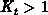 subintervals the error can also
be efficiently suppressed, as is shown in the analysis below.
subintervals the error can also
be efficiently suppressed, as is shown in the analysis below.
In order to estimate the error in the trap occupancy due to the variation of the
carrier concentration 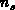 , one has to establish the relationship between the
gate voltage
, one has to establish the relationship between the
gate voltage 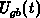 and the concentration
and the concentration 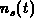 . Hence, an instantaneous
response of the minority and majority carriers to the gate-bias changes is
assumed. Also,
. Hence, an instantaneous
response of the minority and majority carriers to the gate-bias changes is
assumed. Also, 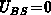 and
and 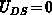 (uniform conditions along the
interface). From the relationship between the surface potential
(uniform conditions along the
interface). From the relationship between the surface potential 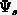 and
and
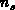 it follows
it follows
The general relationship between the surface potential and the gate voltage yields the expression
where 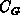 is the total gate capacitance of MOS structure per unit area and
is the total gate capacitance of MOS structure per unit area and
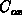 is the oxide capacitance per unit area. To obtain some quantitative
estimations we assume constant bulk doping
is the oxide capacitance per unit area. To obtain some quantitative
estimations we assume constant bulk doping 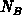 . For depletion and weak
inversion it follows from B.10
. For depletion and weak
inversion it follows from B.10
Finally,
For the same device as in Figure B.2 and
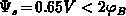 , we have:
, we have: 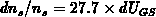 at room
temperatures (
at room
temperatures (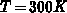 ). A change in
). A change in 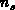 of 3 times corresponds to
of 3 times corresponds to
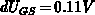 . The restriction on the gate-bias steps becomes stronger at
low temperatures: for
. The restriction on the gate-bias steps becomes stronger at
low temperatures: for 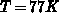 ,
, 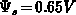 and
and 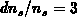 one
obtains
one
obtains 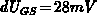 .
.
The linear change of 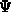 between two time steps is a good approximation when
large changes of the concentrations occur. Therefore,
between two time steps is a good approximation when
large changes of the concentrations occur. Therefore, 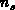 is exponentially
interpolated within the time intervals
is exponentially
interpolated within the time intervals 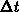 which are used to solve the
basic semiconductor equations. By dividing
which are used to solve the
basic semiconductor equations. By dividing 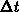 into
into  subintervals,
we effectively reduce the applied gate-bias steps
subintervals,
we effectively reduce the applied gate-bias steps 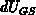 to
to 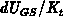 ,
with respect to the discretization error in the trap-dynamics equation. An
example given in Figure B.3 demonstrates the effectiveness of this
method to control the time discretization error in solving the trap-dynamics
equations, which costs a moderate increase in computational effort. For the
example considered in Figure B.3 we obtain for
,
with respect to the discretization error in the trap-dynamics equation. An
example given in Figure B.3 demonstrates the effectiveness of this
method to control the time discretization error in solving the trap-dynamics
equations, which costs a moderate increase in computational effort. For the
example considered in Figure B.3 we obtain for
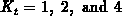 the CPU-times
the CPU-times 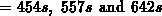
 and the charge-pumping currents
and the charge-pumping currents 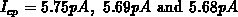 , respectively. An accurate calculation results in
, respectively. An accurate calculation results in
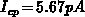 .
.



