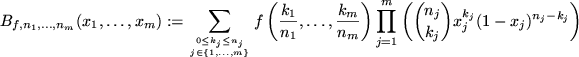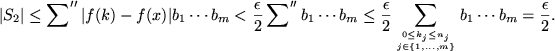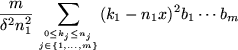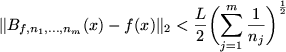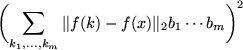B. Multivariate Bernstein Polynomials

Theorem B..1 Let $f: I:=[0,1]\times[0,1]\to\mathbb{R}$ be a continuous function. Then the two-dimensional Bernstein polynomials

$\displaystyle B_{f,n_1,n_2}(x_1,x_2):=\sum_{k_1=0}^{n_1}\sum_{k_2=0}^{n_2} f \l... ... k_1} {n_2\choose k_2} x_1^{k_1} (1-x_1)^{n_1-k_1} x_2^{k_2} (1-x_2)^{n_2-k_2}$

converge pointwise to

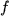
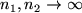
for $n_1,n_2\to\infty$ .

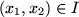
Proof. Let $(x_1,x_2)\in I$ be a fixed point. Because of Theorem 7.2 we have

$\displaystyle {\vert B_{f,n_1,n_2}(x_1,x_2)-f(x_1,x_2)\vert}$
	$\displaystyle \le$	$\displaystyle \vert B_{f,n_1,n_2}(x_1,x_2)-B_{f(.,x_2),n_1}(x_1)\vert + \vert B_{f(.,x_2),n_1}(x_1)-f(x_1,x_2)\vert$
	$\displaystyle \le$	$\displaystyle 2\epsilon$

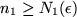
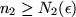
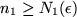
for all $n_1\ge N_1(\epsilon)$ and $n_2\ge N_2(\epsilon)$ . The second summand is smaller than $\epsilon$ for $n_1\ge N_1(\epsilon)$ because

$\displaystyle B_{f(.,x_2),n_1}(x_1) = \sum_{k_1=0}^{n_1} f \left( {k_1\over n_1}, x_2 \right) {n_1\choose k_1} x_1^{k_1} (1-x_1)^{n_1-k_1}$

is the Bernstein polynomial for

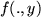
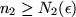
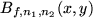
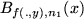
, and the first summand is smaller than $\epsilon$ for $n_2\ge N_2(\epsilon)$ because $B_{f,n_1,n_2}(x,y)$ is the (one-dimensional) Bernstein polynomial for $B_{f(.,y),n_1}(x)$ . Q.E.D.

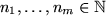
Definition B..2 (Multivariate Bernstein Polynomials) Let $n_1,\ldots,n_m\in\mathbb{N}$ and

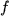
be a function of

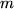
variables. The polynomials

$\displaystyle B_{f,n_1,\ldots,n_m}(x_1,\ldots,x_m):= \sum_{{0\le k_j\le n_j}\at... ...ght) \prod_{j=1}^m \left( {n_j\choose k_j} x_j^{k_j} (1-x_j)^{n_j-k_j} \right)$

are called the multivariate Bernstein polynomials of

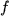
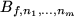
Theorem B..3 (Pointwise Convergence) Let $f: [0,1]^m\to\mathbb{R}$ be a continuous function. Then the multivariate Bernstein polynomials $B_{f,n_1,\ldots,n_m}$ converge pointwise to

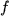
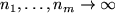
for $n_1,\ldots,n_m\to\infty$ .

Proof. By applying Theorem 7.2 to each summand in

$\displaystyle {\vert B_{f,n_1,\ldots,n_m}(x_1,\ldots,x_m)-f(x_1,\ldots,x_m)\vert}$
	$\displaystyle \le$	$\displaystyle \vert B_{f,n_1,\ldots,n_m}(x_1,\ldots,x_m) - B_{f(.,\ldots,.,x_m),n_1,\ldots,n_{m-1}}(x_1,\ldots,x_{m-1})\vert$
		$\displaystyle {} + \vert B_{f(.,\ldots,.,x_m),n_1,\ldots,n_{m-1}}(x_1,\ldots,x_{m-1}) - B_{f(.,\ldots,.,x_{m-1},x_m),n_1,\ldots,n_{m-2}}(x_1,\ldots,x_{m-2})\vert$
		$\displaystyle {} + \cdots + \vert B_{f(.,x_2,\ldots,x_m),n_1}(x_1) - f(x_1,\ldots,x_m)\vert$

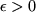
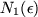
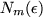
we see that given an $\epsilon>0$ there are $N_1(\epsilon)$ ,..., $N_m(\epsilon)$ such that

$\displaystyle \vert B_{f,n_1,\ldots,n_m}(x_1,\ldots,x_m)-f(x_1,\ldots,x_m)\vert \le m\epsilon$

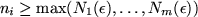
for all $n_i\ge\max(N_1(\epsilon),\ldots,N_m(\epsilon))$ . Q.E.D.

Lemma B..4 For all $x\in\mathbb{R}$

$\displaystyle \sum_{k=0}^{n} (k-nx)^2 {n\choose k} x^k (1-x)^{n-k} = nx(1-x).$

For all $x\in[0,1]$ we have $x(1-x)\le 1/4$ and hence

$\displaystyle 0 \le \sum_{k=0}^{n} (k-nx)^2 {n\choose k} x^k (1-x)^{n-k} \le {n\over 4}.$

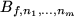
Theorem B..5 (Uniform Convergence) Let $f: [0,1]^m\to\mathbb{R}$ be a continuous function. Then the multivariate Bernstein polynomials $B_{f,n_1,\ldots,n_m}$ converge uniformly to

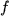
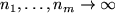
for $n_1,\ldots,n_m\to\infty$ .

Proof. We first note that because of the uniform continuity of

we have

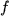
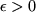
$\displaystyle \forall \epsilon>0:\quad \exists \delta>0:\quad \forall x,x'\in I... ... x-x'\Vert<\delta \;\Longrightarrow\;\Vert f(x)-f(x')\Vert < {\epsilon\over2}.$

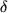
Given an $\epsilon>0$ , we can find such a $\delta$ . In order to simplify notation we set

$\displaystyle b_j:={n_j\choose k_j} x_j^{k_j} (1-x_j)^{n_j-k_j}$

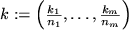
and $k:=\left( {k_1\over n_1}, \ldots, {k_m\over n_m} \right)$ .

always lies in

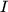
. We have to estimate

$\displaystyle B_{f,n_1,\ldots,n_m}(x) - f(x) = \sum_{{0\le k_j\le n_j}\atop{j\in\{1,\ldots,m\}}} (f(k) - f(x)) b_1\cdots b_m$

and to that end we split the sum into two parts, namely

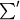
$\displaystyle S_1:= \sum\nolimits' (f(k) - f(x)) b_1\cdots b_m,$

where $\sum\nolimits'$ means summation over all

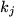
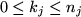
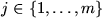
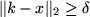
with ${0\le k_j\le n_j}$ (where $j\in\{1,\ldots,m\}$ ) and $\Vert k - x \Vert _2 \ge \delta$ , and

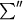
$\displaystyle S_2:= \sum\nolimits'' (f(k) - f(x)) b_1\cdots b_m,$

where $\sum\nolimits''$ means summation over the remaining terms. For

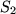
we have

$\displaystyle \vert S_2\vert \le \sum\nolimits'' \vert f(k) - f(x)\vert b_1\cdo... ...{{0\le k_j\le n_j}\atop{j\in\{1,\ldots,m\}}} b_1\cdots b_m = {\epsilon\over2}.$

We will now estimate

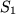
. In the sum

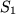
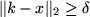
the inequality $\Vert k - x \Vert _2 \ge \delta$ holds, i.e.,

$\displaystyle \left( {k_1\over n_1} - x_1 \right)^2 + \cdots + \left( {k_m\over n_m} - x_m \right)^2 \ge \delta^2.$

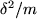
Hence at least one of the summands on the left hand side is greater equal $\delta^2/m$ . Without loss of generality we can assume this is the case for the first summand:

$\displaystyle 1 \le {m\over\delta^2}{(k_1-n_1 x)^2\over n_1^2}.$

Thus, using Lemma B.4,

$\displaystyle \sum\nolimits' b_1\cdots b_m$	$\displaystyle \le$	$\displaystyle \sum\nolimits' {m\over\delta^2 n_1^2} (k_1-n_1 x)^2 b_1\cdots b_m$
	$\displaystyle \le$	$\displaystyle {m\over\delta^2 n_1^2} \sum_{{0\le k_j\le n_j}\atop{j\in\{1,\ldots,m\}}} (k_1-n_1 x)^2 b_1\cdots b_m$
	$\displaystyle =$	$\displaystyle {m\over\delta^2 n_1^2} \sum_{k_1=0}^{n_1} (k_1-n_1 x)^2 {n_1\choose k_1} x_1^{k_1} (1-x_1)^{n_1-k_1}$
	$\displaystyle \le$	$\displaystyle {m\over\delta^2 n_1^2} {n\over4} = {m \over 4 \delta^2 n_1}.$

We can now estimate

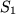
. Since

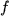
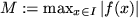
is continuous on a compact set $M:=\max_{x\in I} \vert f(x)\vert$ exists.

$\displaystyle \vert S_1\vert$	$\displaystyle \le$	$\displaystyle \sum\nolimits' \vert f(k) - f(x)\vert b_1\cdots b_m$
	$\displaystyle \le$	$\displaystyle 2M \sum\nolimits' b_1\cdots b_m$
	$\displaystyle \le$	$\displaystyle {2Mm\over4\delta^2 n_1} = {Mm\over2\delta^2 n_1}$

For

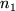
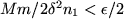
large enough we have $Mm / 2\delta^2n_1 < \epsilon/2$ and thus

$\displaystyle \vert B_{f,n_1,\ldots,n_m}(x) - f(x)\vert \le \vert S_1\vert+\vert S_2\vert < {\epsilon\over2} + {\epsilon\over2} = \epsilon,$

which completes the proof. Q.E.D.

Corollary B..6 The set of all polynomials is dense in

Theorem B..7 (Error Bound for Lipschitz Condition) If $f: I:=[0,1]^m\to\mathbb{R}$ is a continuous function satisfying the Lipschitz condition

$\displaystyle \Vert f(x)-f(y)\Vert _2 < L \Vert x-y\Vert _2$

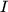
, then the inequality

$\displaystyle \Vert B_{f,n_1,\ldots,n_m}(x) - f(x) \Vert _2 < {L\over2} \biggl( \sum_{j=1}^m {1\over n_j} \biggr)^{1\over2} %$

holds.

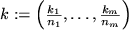
Proof. Abbreviating notation we set $k:=\left( {k_1\over n_1}, \ldots, {k_m\over n_m} \right)$ . We will use the Lipschitz condition, Corollary A.7, and Lemma B.4.

$\displaystyle {\Vert B_{f,n_1,\ldots,n_m}(x) - f(x) \Vert _2^2}$
	$\displaystyle \le$	$\displaystyle \biggl( \sum_{k_1,\ldots,k_m} \Vert f(k) - f(x) \Vert _2 b_1\cdots b_m \biggr)^2$
	$\displaystyle <$	$\displaystyle \left( L \sum \Vert k-x \Vert _2 b_1\cdots b_m \right)^2$
	$\displaystyle \le$	$\displaystyle L^2 \left( \sum \Vert k-x \Vert _2^2 b_1\cdots b_m \right) \left( \sum b_1\cdots b_m \right)$
	$\displaystyle =$	$\displaystyle L^2 \sum \left( \left({k_1\over n_1}-x_1\right)^2 + \cdots + \left({k_m\over n_m}-x_m\right)^2 \right) b_1\cdots b_m$
	$\displaystyle =$	$\displaystyle L^2 \sum_{j=1}^m {x_j(1-x_j)\over n_j}$
	$\displaystyle \le$	$\displaystyle L^2 \sum_{j=1}^m {1\over 4 n_j}$

This completes the proof. Q.E.D.

Theorem B..8 (Asymptotic Formula) Let $f: I:=[0,1]^m\to\mathbb{R}$ be a

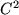
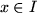
function and $x\in I$ , then

$\displaystyle \lim_{n\to\infty} n ( B_{f,n,\ldots,n}(x) - f(x) ) = \sum_{j=1}^m... ...rtial x_j^2} \le {1\over8} \sum_{j=1}^m {\partial ^2 f(x)\over\partial x_j^2}.$

Proof. We define the vector

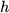
through

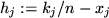
, where the

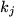
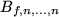
are the integers over which we sum in $B_{f,n,\ldots,n}$ . Using Theorem A.14 we see

$\displaystyle f\left({k_1\over n},\ldots,{k_m\over n}\right)$	$\displaystyle =$	$\displaystyle f(x) + \sum_{j=1}^m \left( {k_j\over n}-x_j \right) {\partial f(x)\over\partial x_j}$
		$\displaystyle {} + {1\over2} \sum_{i=1}^m\sum_{j=1}^m \left( {k_i\over n}-x_i \... ...) {\partial ^2 f(x_0)\over \partial x_i \partial x_j} + \Vert h\Vert^2 \rho(h),$

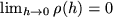
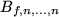
where $\lim_{h\to0} \rho(h)=0$ . Summing this equation like the sum in $B_{f,n,\ldots,n}$ we obtain

$\displaystyle B_{f,n,\ldots,n} = f(x) + {1\over2} \sum_{i=1}^m {x_j(1-x_j)\over... ...r \partial x_j^2} + \sum_{k_1,\ldots,k_m} \Vert h\Vert^2 \rho(h) b_1\cdots b_m$

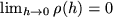
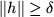
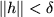
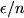
since many terms vanish or can be summed because of Lemma B.4. Noting $\lim_{h\to0} \rho(h)=0$ we can apply the same technique as in the proof of Theorem B.5 for estimating the last sum in the last equation, i.e., splitting the sum into two parts for $\Vert h\Vert\ge\delta$ and $\Vert h\Vert<\delta$ . Hence we see that for all $\epsilon$ this sum is less equal $\epsilon/n$ for all sufficiently large

, which yields the claim. Q.E.D.