| (2.58) |
Our first implementation used a mobility model which was originally introduced by Hänsch. The higher order parameters used were found by fitting data from Monte Carlo simulations. It is a specialization of a more general model which has been implemented in MINIMOS-NT.
Define (lattice scattering, lattice impurity scattering):
| (2.58) |
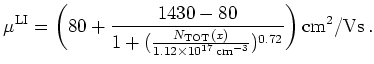 |
(2.59) |
Here
![]() is the net doping, i.e.,
is the net doping, i.e.,
| (2.60) |
Then using the form
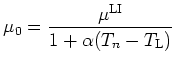 |
(2.61) |
where
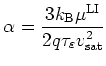 |
(2.62) |
with the saturation velocity in silicon
| (2.63) |
we get
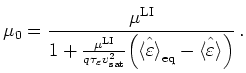 |
(2.64) |
For the higher mobilities we use
| (2.65) |
| (2.66) |
For the relaxation times we use
| (2.67) |
This analytical model gives good results on some practical examples. In the production version of MINIMOS-NT we take a different approach. We use tables for the mobilities and relaxation times. These tables are extracted from Monte Carlo data in such a way that the six moments model gives identical results for the bulk case. See Section 2.3.4 for details.
![]()
![]()
![]()
![]() Previous: 2.3.2 Odd Moments: Mobilities
Up: 2.3 Closure Relations for
Next: 2.3.4 Consistency with Bulk
Previous: 2.3.2 Odd Moments: Mobilities
Up: 2.3 Closure Relations for
Next: 2.3.4 Consistency with Bulk