 |
Die Methode der finiten Elemente wurde ursprünglich zur ingenieursmäßigen Berechnung mechanischer Probleme bereits Anfang der 40er Jahre entwickelt. Die konsequente Weiterentwicklung der Methode führte zu einer allgemein verwendbaren Diskretisierungsmethode für partielle Differentialgleichungen im Kontinuum (ein geschichtlicher Überblick ist in [Zie89] zu finden).
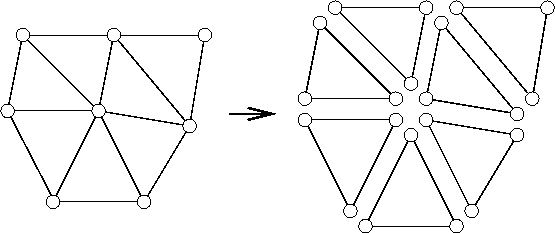
Bei der Methode der finiten Elemente ist die Form und die geographische Lage der Elemente durch die Ortskoordinaten der Knoten vollständig festgelegt. Mit diesen intrinsisch im Element vorhandenen Informationen können alle im Element benötigten Operationen zur Berechnung der diskreten Differentialoperatoren durchgeführt werden. Die Gesamtgleichung entsteht durch die additive Überlagerung der elementweisen diskreten Operatoren indem die Elemente gemeinsame Knoten referenzieren. Es ist dies der sogenannte Vorgang der Assemblierung des globalen Gleichungssystems (siehe Kap. 4.5). Abb. 4.2 stellt die elementweise Abarbeitung des Gitters anschaulich dar.
Während in vielen Implementierungen der FBM auf unstrukturierten Gittern Linienelemente zur Darstellung der Kopplung zwischen zwei Knoten verwendet werden, sind bei der FEM allgemeinere Elemente mit höherer Knotenanzahl üblich. Die einfachsten Vertreter sind das Dreieck im zweidimensionalen und der Tetraeder im dreidimensionalen Raum, welche durch die Ortskoordinaten der drei beziehungsweise vier Knoten definiert sind.
Die lokale Verfügbarkeit aller notwendigen Daten zwingt förmlich einen objektorientierten Ansatz auf und erleichtert damit die Implementierung eines allgemein verwendbaren Programms, welches prinzipiell keine Einschränkungen hinsichtlich der Art der zu lösenden Differentialgleichung und der einsetzbaren Elementtypen notwendig macht. Auch Problemstellungen mit ortsveränderlichen Gittern lassen sich direkt und ohne großen Aufwand implementieren, da die geometrischen Koeffizienten des Elementes ohnehin lokal zum Zeitpunkt der Assemblierung ermittelt werden. Es müssen lediglich die Automatismen zur Verwaltung von Funktionswerten mehrerer diskreter Zeitpunkte, die für die Näherungslösungen ohnehin erforderlich sind, auch auf die Ortskoordinaten der Knoten anwendbar sein.
Weiters zeigt eine nähere Betrachtung der Methode, daß die FBM mittels der FEM abgebildet werden kann, wenn die geometrischen Kopplungkoeffizienten in der gleichen Weise wie für die FBM ermittelt werden. Die beiden Methoden unterscheiden sich dann lediglich in der Reihenfolge der Summation der einzelnen Beiträge, was im folgenden anhand eines Dreiecksgitters dargestellt wird.
Die Berandung der Voronoi-Boxen besteht aus den Liniensymmetralen der Gitterlinien. Der
Kopplungsquerschnitt Aij=kij1+kij2 (vlg. Gl. 4.4) entspricht dabei
dem Abstand zwischen den Umkreismittelpunkten der an der Linie angrenzenden Dreiecke
(Abb. 4.3) und kann aus den Abständen kij1 und kij2 der Umkreismittelpunkte
M1 und M2 zum Linienmittelpunkt ML berechnet werden. Es ist dabei lediglich darauf zu
achten, daß die Abstände vorzeichenrichtig berechnet werden, denn liegt der Umkreismittelpunkt
außerhalb des Dreieckes, ist der Abstand negativ. Gl. 4.4 kann dann auch durch
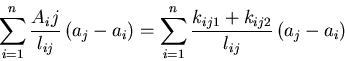 |
(4.5) |
Nachdem die elementweise Abarbeitung des Gitters sowohl die Implementierung der Boxintegration als auch die Implementierung der FEM erlaubt, wurde das im Zuge der vorliegenden Arbeit erstellte Programm dementsprechend strukturiert.