


Next: 3.1.6 Boundary Conditions
Up: 3.1 Sets of Partial
Previous: 3.1.4 The Lattice Heat
In insulating materials only the Poisson equation
(3.1) and the lattice heat flow equation (3.14)
are solved. The presence of doping and mobile carriers is neglected
(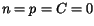 ), therefore the carrier continuity equations are not solved. This
assumption leads to the reduction of (3.1) to the
Laplace equation (3.18) and the neglecting
of the heat generation term of (3.14), which is invoked for
semiconductor segments only.
), therefore the carrier continuity equations are not solved. This
assumption leads to the reduction of (3.1) to the
Laplace equation (3.18) and the neglecting
of the heat generation term of (3.14), which is invoked for
semiconductor segments only.
| |
|
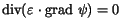 |
(3.18) |
| |
|
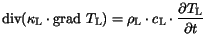 |
(3.19) |
Thus, as a result no currents flow through insulators and the influence of the
charges inside the insulators is neglected. This assumptions can be neglected,
in case of the insulator is treated as a semiconductor material. This approach
was successfully applied to Si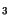 N
N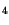 and shall be illustrated later in this
work. Another approach is the consideration of charges at the
semiconductor/insulator interface, which is discussed in the next subsection.
and shall be illustrated later in this
work. Another approach is the consideration of charges at the
semiconductor/insulator interface, which is discussed in the next subsection.



Next: 3.1.6 Boundary Conditions
Up: 3.1 Sets of Partial
Previous: 3.1.4 The Lattice Heat
Vassil Palankovski
2001-02-28