By expanding the GREEN's function in terms of the basis functions the
continuity equation (3.87) can be derived as
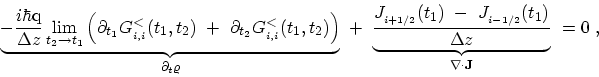 |
(4.52) |
where
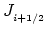 represents the current passing through a point between
represents the current passing through a point between 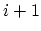 and
and 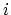 .
Note that
.
Note that 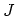 has a unit of
has a unit of
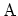 rather than
rather than
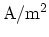 due to the
one-dimensional nature of CNTs. The time derivative of the GREEN's functions
can be replaced by the relation (3.62)
due to the
one-dimensional nature of CNTs. The time derivative of the GREEN's functions
can be replaced by the relation (3.62)
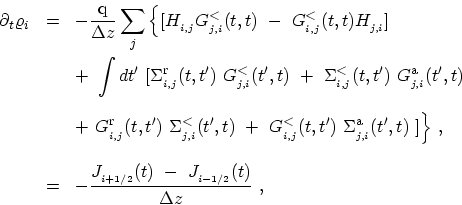 |
(4.53) |
where the term inside the integral is zero due to the condition stated
in (3.90).
The next step is separating
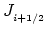 from
from
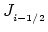 by
decomposing equation (4.52). CAROLI proposed the following ansatz
in [96]. The current
by
decomposing equation (4.52). CAROLI proposed the following ansatz
in [96]. The current 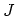 is the difference between the flow of particles from left to right
and from right to left. This leads to the following expression for
is the difference between the flow of particles from left to right
and from right to left. This leads to the following expression for
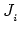 [96]
[96]
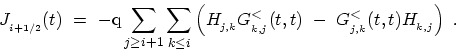 |
(4.54) |
It is straightforward to show that (4.54) along with an expression for
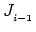 satisfies (4.53).
satisfies (4.53).
Under steady-state condition one can transform the time difference
coordinate to energy to obtain
![\begin{displaymath}\begin{array}{ll}\displaystyle J_{_{i+1/2}} \ &\displaystyle ...
...\ 2\ \Re \mathrm{e}[ H_{_{j,k}}G^<_{_{k,j}}(E)] \ , \end{array}\end{displaymath}](img875.png) |
(4.55) |
Based on the nearest neighbor tight-binding method in mode-space (see Section 4.4)
equation (4.55) can be simplified to
![\begin{displaymath}\begin{array}{l}\displaystyle J^{^\nu}_{_{i+1/2}} \ = \ \frac...
... {t}^{^\nu}_{_{i+1,i}} {G}^{<^\nu}_{_{i,i+1}}]\ \ , \end{array}\end{displaymath}](img876.png) |
(4.56) |
where the summation runs over all the subbands contributing to transport.
The factor 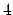 in (4.56) is due to double spin and double subband degeneracy.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
in (4.56) is due to double spin and double subband degeneracy.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() from
from
![]() by
decomposing equation (4.52). CAROLI proposed the following ansatz
in [96]. The current
by
decomposing equation (4.52). CAROLI proposed the following ansatz
in [96]. The current ![]() is the difference between the flow of particles from left to right
and from right to left. This leads to the following expression for
is the difference between the flow of particles from left to right
and from right to left. This leads to the following expression for
![]() [96]
[96]