| si = s(xi), 1 |
(B1) |
For a set of data points
| si = s(xi), 1 |
(B1) |
the interpolation function is defined as
| s(x) = a0 + a1 . (x - xi) + a2 . (x - xi)2 + a3 . (x - xi)3, xi |
(B2) |
To determine the coefficients a0, a1, a2, and a3 of the interpolation polynomial for each interval [xi, xi + 1] the function values si and si + 1, and the first derivatives si' and si + 1' at the end points of the interval are used.
The first derivative si' of the interpolation function at xi is estimated from the data for this point and the next two points on each side of xi. Using the ratios
| dj = |
(B3) |
and the weighting coefficients
| wi - 1 | = | di + 1 - di|, | (B4) |
| wi | = | di - 1 - di - 2|, | (B5) |
the estimated derivative si' is defined as
Several special cases for si' have to be considered.
| si' | = di - 1 | di - 2 = di - 1, di |
(B7) | |
| si' | = di | di = di + 1, di - 2 |
(B8) | |
| si' | = di - 1 = di | di - 1 = di | (B9) | |
| si' | = 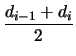 |
di - 2 = di - 1 |
(B10) |
To be able to use (B.6) for calculating the derivatives s1', s2', sk - 1', and sk' additional ratios d-1, d0, dk, and dk + 1 have to be estimated.
| d-1 | = 2 . d0 - d1 | (B11) |
| d0 | = 2 . d1 - d2 | (B12) |
| dk | = 2 . dk - 1 - dk - 2 | (B13) |
| dk + 1 | = 2 . dk - dk - 1 | (B14) |
The order of the interpolation function reduces to 2 for these intervals.
Similar algorithms can be used for the interpolation of two-dimensional data on rectangular grids [43] and on unstructured grids[44] by bicubic and cubic polynomials, respectively.