


Next: 3. Topography Effects in
Up: Dissertation Alireza Sheikholeslami
Previous: 1. Introduction
Subsections
2. Mathematical Description of the Motion of Interfaces
In this chapter we present PDE s which
describe moving interfaces. From one point of
view this leads to a boundary value problem for a PDE and from another point of view to
a time-dependent initial value problem for a PDE. We also lay out the theoretical and
computational advantages of these two formulations.
2.1 Formulation of the Motion of Interfaces
In order to describe a moving boundary in direction
normal to the boundary
(we neglect the tangential component of the speed, because the
addition of a tangential component has the effect of just changing the
parameterization of the boundary [71]) one has to know
the value of the normal speed function which we denote as 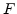 . The speed function
. The speed function
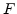 generally depends on many parameters and can be written as
generally depends on many parameters and can be written as 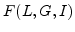 , where
, where
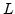 ,
, 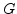 , and
, and 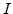 stand for local, global, and independent
parameters described as follows:
stand for local, global, and independent
parameters described as follows:
- Local parameters are determined by geometric informations, e.g.,
normal vector and curvature.
- Global parameters are determined by shape and position of the
interface.
- Independent parameters are independent of the shape of the interfaces,
such as an underlying fluid velocity that passively transports the front.
For the moment we assume that 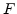 is
known and our goal is to track and describe the motion of interface.
is
known and our goal is to track and describe the motion of interface.
2.1.1 The Boundary Value Formulation
Assuming 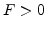 , the interface will always move outward. One way to
detect the position of the interface is to find the time
, the interface will always move outward. One way to
detect the position of the interface is to find the time 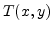 at which
the interface crosses a point with coordinates
at which
the interface crosses a point with coordinates 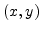 . Considering the
fact that in one dimension distance is equal to speed multiplied by
time, the equation of motion of the interface can be formulated as follows:
In multiple dimensions
. Considering the
fact that in one dimension distance is equal to speed multiplied by
time, the equation of motion of the interface can be formulated as follows:
In multiple dimensions 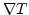 is orthogonal to level sets of
is orthogonal to level sets of 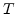 and analogous to one dimension it is inversely proportional to
and analogous to one dimension it is inversely proportional to
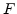 . Therefore, we can write
. Therefore, we can write
 |
(2.1) |
where
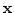 is the initial position of the interface. Hence, this
formulation of motion of an interface leads to a boundary value
problem.
is the initial position of the interface. Hence, this
formulation of motion of an interface leads to a boundary value
problem.
2.1.2 The Initial Value Formulation
In contrast to the requirement of 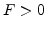 , the speed is not strictly
positive but it can be arbitrarily positive or negative. This leads to a motion of
the interface backward and forwards. Therefore, the interface can pass a
certain point more than one time. Therefore,
, the speed is not strictly
positive but it can be arbitrarily positive or negative. This leads to a motion of
the interface backward and forwards. Therefore, the interface can pass a
certain point more than one time. Therefore, 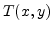 is no
unique value to detect the position of the interface. In
order to solve this problem we embed the initial position of the interface
as the zero level set of a function
is no
unique value to detect the position of the interface. In
order to solve this problem we embed the initial position of the interface
as the zero level set of a function 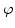 in a higher dimension. Linking the
position of the interface to the evolution of
in a higher dimension. Linking the
position of the interface to the evolution of 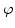 leads to a
time-dependent initial value problem. At each time step the interface is
given by the zero level set of the time-dependent level set function
leads to a
time-dependent initial value problem. At each time step the interface is
given by the zero level set of the time-dependent level set function
 .
.
To derive the equation of motion, we define the interface
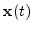 which must always guarantee the following equation
which must always guarantee the following equation
Using the chain rule the above equation results in
Since the normal vector
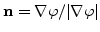 , and
, and
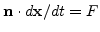 , we get the level set equation in the
following form [80]:
, we get the level set equation in the
following form [80]:
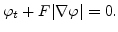 |
(2.2) |
2.1.3 The Beneficial Properties and Comparison of These Formulations
Some common advantages of the boundary and initial value problem are
listed [80] here:
- The topological changes of the interface are handled very well. Since the
position of interface is given either by the zero level set of
the level set function or by the level set
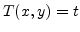 in each time, which are
single-value functions, the interface need not be a single boundary
and it can break and merge as
in each time, which are
single-value functions, the interface need not be a single boundary
and it can break and merge as  proceeds.
proceeds.
- The geometrical quantities such as normal vector and curvature
can be determined easily.
- They are very efficient because of the possibility to use fast
marching and narrow
banding methods which will be discussed
in Section 5.5 and in Section 5.6, respectively.
At the same time there are important differences between these two
formulations [80]:
- Because of the ability of the initial value formulation to
accept positive and negative
speeds, models with
complex speed functions, e.g., curvature dependent speed, are
handled with initial value formulation and not with the boundary
value formulation.
- In contrast to the initial value formulation, the boundary value formulation
requires no time stepping and does therefore not depend on a CFL
(Courant-Friedrichs-Levy) condition which will be discussed in
Section 5.13.
- The boundary value formulation enables to use a fast marching method
which is very efficient2.1.
2.2 An Overview of the Techniques for Tracking the
Motion of a Surface
Various surface representation algorithms beside the level set method have been used to
develop topography simulators. Roughly speaking, these
algorithms fall into two categories [53], namely, string-based
and cell-based methods. In the next sections we briefly present these three methods.
Figure 2.1:
Illustration of the representation of a boundary by
string-based method.
|
|
2.2.1 String-Based Methods
This approach has also been known under different names such as marker
particle, nodal, and string method [97,72]. The
interface is represented as a series of lines in two dimensions (cf.
Figure 2.1) or triangle segments in three dimensions. The position of
nodes forming a line or triangle segment is advanced in each time
step using interface information about the normals and curvatures of
the surface facets. Several techniques have to be used for an
accurate advancement of the interface, while at the same time keeping the CPU time at a minimum. For this
purpose the number of nodes needs to be kept at a minimum. In
order to do this the nodes have to be distributed as a
function of the curvature. Thus the flat part of the interface only
requires one line segment independent of its length. While this
can be easily achieved, during the advance of neighboring
surface facets along their normals, interstices or duplications occur
and thus area-readjustment procedures for de-looping are needed. However, these procedures induce significant
computational error into the simulation result in proportion to the
complexity of the process geometry. Furthermore, these methods are
very time and memory consuming in three dimensions and strongly limit the
applicability of these methods in three
dimensions.
Figure 2.2:
Illustration of the representation of a boundary by
cell-based method.
|
|
2.2.2 Cell-Based Methods
This method has also been introduced under different names such as
partial fraction or cell method
[65,64]. Considering a grid within a computational
domain, a basic idea of this method is to assign values to each grid
cell depending on the fractional part of the cell containing the
interface. Therefore, grid cells which are totally lying within or outside the
interface get 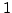 or 0, respectively. The grid cells containing a
part of interface get a value between 0 and
or 0, respectively. The grid cells containing a
part of interface get a value between 0 and  . These grid cells
are called surface cells as shown in Figure 2.2. After advancing the
interface, the fractional values are updated where the interface is detected. The main advantages of this approach
are its robustness and good handling of critical structures such as
high aspect ratio trenches used in simulations. There are some disadvantages, however:
. These grid cells
are called surface cells as shown in Figure 2.2. After advancing the
interface, the fractional values are updated where the interface is detected. The main advantages of this approach
are its robustness and good handling of critical structures such as
high aspect ratio trenches used in simulations. There are some disadvantages, however:
- Calculation of geometrical quantities such as surface normals
and curvatures is inaccurate.
- Since the accuracy of the localization of the interface based on
fractional values strongly depends on the grid resolution, a high
grid resolution is needed to extract the interface reliably.
At our institute Dr. Pyka has implemented a
topography simulator based on the method described
above. The simulator has been used to rigorously treat
different etching and deposition models. Furthermore, it has been used
to generate accurate input geometries to guarantee reliable
interconnect or device analysis [64].
Figure 2.3:
Illustration of the idea of the level set method. The curve on
the left is the original curve in 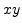 plane. This curve is built
into a cone-shaped surface, namely, the level set function as
shown on the right. The intersection of the level set function
with
plane. This curve is built
into a cone-shaped surface, namely, the level set function as
shown on the right. The intersection of the level set function
with 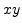 plane in each time step gives the curve.
plane in each time step gives the curve.
|
|
2.2.3 Level-Set-Based Methods
The level set method [80] is an interesting
alternative method that solves the previously mentioned
problems emerging with the other methods.
It provides means to describe
boundaries, i.e., curves, surfaces or hyper-surfaces in arbitrary
dimensions, and their evolution in time which is caused
by forces or fluxes normal to the surface. The basic idea is to view
the curve or surface in question at a certain time 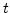 as the zero
level set (with respect to the space variables) of a certain function
as the zero
level set (with respect to the space variables) of a certain function
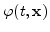 , the so called level set function as shown in Figure 2.3. Thus the initial
surface is the set
, the so called level set function as shown in Figure 2.3. Thus the initial
surface is the set
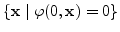 .
.
Each point on the surface is moved with a certain speed normal to the
surface and this determines the time evolution of the surface. The
speed normal to the surface will be denoted by
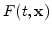 . For
points on the zero level set it is usually determined by physical
models, in our case by etching and deposition processes, or
more precisely by the fluxes of certain gas species and subsequent
surface reactions. The speed function
. For
points on the zero level set it is usually determined by physical
models, in our case by etching and deposition processes, or
more precisely by the fluxes of certain gas species and subsequent
surface reactions. The speed function
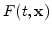 generally depends
on the time and space variables and we assume, for now, that it is
defined on the whole simulation domain and in the whole time interval
considered.
generally depends
on the time and space variables and we assume, for now, that it is
defined on the whole simulation domain and in the whole time interval
considered.
The surface at a later time 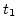 shall also be considered as the zero
level set of the function
shall also be considered as the zero
level set of the function
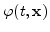 , namely
, namely
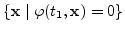 . As we showed in (2.2) with some
notational differences, this leads to the level set equation
. As we showed in (2.2) with some
notational differences, this leads to the level set equation
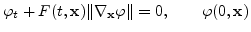 given given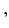 |
(2.3) |
in the unknown function 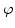 , where
, where
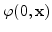 determines the initial
surface. Having solved this equation, the zero level set of the
solution is the sought curve or surface at all later times.
determines the initial
surface. Having solved this equation, the zero level set of the
solution is the sought curve or surface at all later times.
Although in the numerical application the level set function is
eventually calculated on a grid, the resolution achieved is in fact
much higher than the resolution of the grid, and hence higher than the
resolution achieved using a cellular algorithm on a grid of the same resolution.
This is due to the surface extraction step, where
the curve or surface is reconstructed by lines or triangles using
linear interpolation of the level set values on the grid. Of course the level set
function must essentially remain a linear function near to the zero level set.
Foonotes
- ... efficient2.1
- Fast marching method is
principally used by the boundary value formulation, but it can be
used for the calculation of the distance function when using the initial
value formulation.



Next: 3. Topography Effects in
Up: Dissertation Alireza Sheikholeslami
Previous: 1. Introduction
A. Sheikholeslami: Topography Simulation of Deposition and Etching Processes
![]() which must always guarantee the following equation
which must always guarantee the following equation
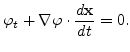
![]() , and
, and
![]() , we get the level set equation in the
following form [80]:
, we get the level set equation in the
following form [80]:
![\includegraphics[width=\linewidth]{level_set_embedding}](img105.png)
![]() . For
points on the zero level set it is usually determined by physical
models, in our case by etching and deposition processes, or
more precisely by the fluxes of certain gas species and subsequent
surface reactions. The speed function
. For
points on the zero level set it is usually determined by physical
models, in our case by etching and deposition processes, or
more precisely by the fluxes of certain gas species and subsequent
surface reactions. The speed function
![]() generally depends
on the time and space variables and we assume, for now, that it is
defined on the whole simulation domain and in the whole time interval
considered.
generally depends
on the time and space variables and we assume, for now, that it is
defined on the whole simulation domain and in the whole time interval
considered.
![]() shall also be considered as the zero
level set of the function
shall also be considered as the zero
level set of the function
![]() , namely
, namely
![]() . As we showed in (2.2) with some
notational differences, this leads to the level set equation
. As we showed in (2.2) with some
notational differences, this leads to the level set equation