


Next: 2.5 Selbstkonsistente Lösung
Up: 2. Schrödinger-Poisson-Solver
Previous: 2.3 Erweiterung auf Heterostrukturen
Unterabschnitte
Bei der Betrachtung der Schrödinger-Gleichung haben wir
den Verlauf des Potenzials als bekannt vorausgesetzt.
Dieses Potenzial ist aus der Poisson-Gleichung zu bestimmen.
Beim Übergang zwischen zwei Schichten ergibt sich ein Sprung
in der Dielektrizitätskonstante
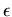 .
Die Raumladungsdichte
.
Die Raumladungsdichte 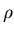 besteht aus mehreren Komponenten.
Für die Beschreibung der ortsfesten Ladungen im Simulationsgebiet
werden die Konzentration der Donatoren und
Akzeptoren,
besteht aus mehreren Komponenten.
Für die Beschreibung der ortsfesten Ladungen im Simulationsgebiet
werden die Konzentration der Donatoren und
Akzeptoren, 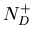 und
und 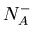 , verwendet.
, verwendet. 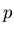 steht für die
Löcherkonzentration.
Bei den Elektronen wird der Beitrag der nicht quantisiert betrachteten
Elektronen durch
steht für die
Löcherkonzentration.
Bei den Elektronen wird der Beitrag der nicht quantisiert betrachteten
Elektronen durch
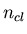 berücksichtigt.
Der Anteil
berücksichtigt.
Der Anteil
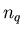 der Elektronenkonzentration wird aus den
Lösungen der Schrödinger-Gleichung berechnet.
der Elektronenkonzentration wird aus den
Lösungen der Schrödinger-Gleichung berechnet.
Die Beschreibung der Ladungsträger erfolgt über diskrete Zustände im
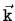 -Raum. Bei der klassischen Betrachtung wird angenommen, dass die
Dichte dieser Zustände ausreicht, um eine kontinuierliche Mittelung vornehmen
zu können. Es wird dabei über alle diskreten Zustände summiert und die
mittlere Ladungsträgerkonzentration wie folgt angeschrieben.
-Raum. Bei der klassischen Betrachtung wird angenommen, dass die
Dichte dieser Zustände ausreicht, um eine kontinuierliche Mittelung vornehmen
zu können. Es wird dabei über alle diskreten Zustände summiert und die
mittlere Ladungsträgerkonzentration wie folgt angeschrieben.
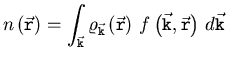 |
(2.66) |
Die Zustandsdichte
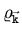 gibt die Dichte der Zustände im
gibt die Dichte der Zustände im
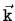 -Raum an und berücksichtigt eine etwaige Entartung der
betrachteten Zustände. Für einen Zustand ergibt sich dabei
unter Berücksichtigung der Entartung
-Raum an und berücksichtigt eine etwaige Entartung der
betrachteten Zustände. Für einen Zustand ergibt sich dabei
unter Berücksichtigung der Entartung
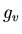 der betrachteten
Talsorte
der betrachteten
Talsorte 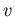 und einem Faktor
und einem Faktor  für die beiden Spinzustände eine
Gesamtentartung von
für die beiden Spinzustände eine
Gesamtentartung von
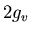 . Bezogen auf das
Einheitsvolumen
. Bezogen auf das
Einheitsvolumen
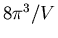 ergibt sich die Zustandsdichte im
ergibt sich die Zustandsdichte im
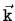 -Raum zu
-Raum zu
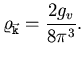 |
(2.67) |
Für die Besetzungswahrscheinlichkeit
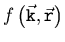 wird die Fermi-Dirac-Statistik
verwendet. Unter Benutzung des Begriffs der Fermi-Energie
wird die Fermi-Dirac-Statistik
verwendet. Unter Benutzung des Begriffs der Fermi-Energie
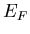 und
der Elektronentemperatur
und
der Elektronentemperatur
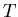 , welche hier mit der Gittertemperatur
gleichgesetzt wird, lautet die Wahrscheinlichkeit für die Besetzung eines
Zustands mit der Energie
, welche hier mit der Gittertemperatur
gleichgesetzt wird, lautet die Wahrscheinlichkeit für die Besetzung eines
Zustands mit der Energie
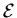
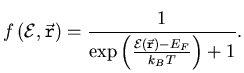 |
(2.68) |
Wir haben nun die Besetzungswahrscheinlichkeit als Funktion der Energie,
die Zustandsdichte jedoch im
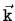 -Raum vorliegen.
Eine Umformung zwischen den beiden Darstellungen kann
über die Teilchenerhaltung erfolgen.
-Raum vorliegen.
Eine Umformung zwischen den beiden Darstellungen kann
über die Teilchenerhaltung erfolgen.
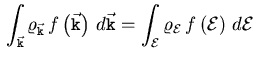 |
(2.69) |
Bei gegebener Dispersionsrelation
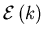 kann die Besetzungswahrscheinlichkeit
kann die Besetzungswahrscheinlichkeit
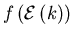 auf der linken Seite
von (2.71) eingesetzt werden, und durch Umformen
der Integrationsvariablen die Zustandsdichte über der Energie
ausgedrückt werden.
auf der linken Seite
von (2.71) eingesetzt werden, und durch Umformen
der Integrationsvariablen die Zustandsdichte über der Energie
ausgedrückt werden.
Für den Wechsel der Integrationsvariablen vom Wellenvektor auf die
Energie bieten sich Polarkoordinaten und damit die Umformung
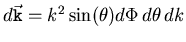 an. Darin laufen
die beiden Winkel
an. Darin laufen
die beiden Winkel 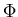 und
und 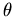 von 0 bis
von 0 bis 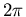 beziehungsweise von 0 bis
beziehungsweise von 0 bis 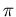 . Bei Verwendung der parabolischen
Dispersionsrelation (2.33) ergibt sich durch
Einsetzen in (2.71) die bekannte Formel
. Bei Verwendung der parabolischen
Dispersionsrelation (2.33) ergibt sich durch
Einsetzen in (2.71) die bekannte Formel
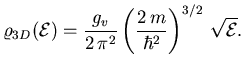 |
(2.70) |
Für die nichtparabolische Dispersionsrelation
nach (1.15) ergibt sich eine vom
Nichtparabolizitätskoeffizienten abhängige Zustandsdichte.
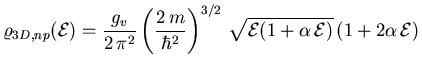 |
(2.71) |
Bei der Berechnung der Trägerkonzentration wollen wir einen hier verwendeten
Spezialfall betrachten, in dem die Integration nicht bei der Energie
der Leitungsbandkante, sondern bei einer höher gelegenen Energie
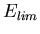 beginnen soll. Auf diese Weise setzt sich die Elektronenkonzentration aus
zwei Beiträgen zusammen, dem klassischen Anteil
beginnen soll. Auf diese Weise setzt sich die Elektronenkonzentration aus
zwei Beiträgen zusammen, dem klassischen Anteil
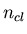 und
einem Anteil
und
einem Anteil
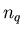 , der aus der Lösung der Schrödinger-Gleichung
berechnet wird.
, der aus der Lösung der Schrödinger-Gleichung
berechnet wird.
Nach Einsetzen der Zustandsdichten (2.72)
und (2.73) in (2.68) ergibt
die Berechnung der Elektronenkonzentration im nicht quantisierten Fall (Index
3D):
Für den nicht parabolischen Fall (Index np) wurde, unter Annahme der bei
Raumtemperatur zu erwartenden Energien und dem in Silizium üblichen
Nichtparabolizitätskoeffizienten, der unter der Wurzel auftretende Term
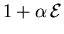 vernachlässigt.
So erhält man im parabolischen und im nicht parabolischen Fall einen Ausdruck,
der die unvollständigen Fermi-Integrale
vernachlässigt.
So erhält man im parabolischen und im nicht parabolischen Fall einen Ausdruck,
der die unvollständigen Fermi-Integrale
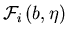 aus
Anhang A.2 verwendet.
Zwecks einfacherer Schreibweise wurden
einige Größen eingeführt, die im weiteren statt der Energie der
Leitungsbandkante, der eben besprochenen Energiebarriere
aus
Anhang A.2 verwendet.
Zwecks einfacherer Schreibweise wurden
einige Größen eingeführt, die im weiteren statt der Energie der
Leitungsbandkante, der eben besprochenen Energiebarriere
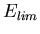 und des
Nichtparabolizitätskoeffizienten verwendet werden.
und des
Nichtparabolizitätskoeffizienten verwendet werden.
Für die zweidimensionale Ladungsträgerkonzentration ist die Bewegung in einer Raumrichtung
quantisiert und die Ladungsträgerkonzentration wird in dieser Richtung über
die einhüllenden Funktionen
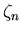 aus dem
Separationsansatz (2.4) beschrieben. Die Dichte
der Zustände in einer Ebene des
aus dem
Separationsansatz (2.4) beschrieben. Die Dichte
der Zustände in einer Ebene des
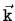 -Raumes beträgt
-Raumes beträgt
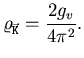 |
(2.74) |
Im Integral (2.71) wird nur der Anteil aus der Bewegung
in der Parallelrichtung betrachtet. Bei der Umwandlung zwischen
der Energie und der Parallelkomponente des Wellenvektors folgt aus
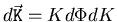 und der parabolischen
Dispersionsrelation eine konstante Dichte. Bei Berücksichtigung der
nichtparabolischen Korrektur ergibt sich aus der Ableitung der Energie
nach dem Wellenvektor der Faktor
und der parabolischen
Dispersionsrelation eine konstante Dichte. Bei Berücksichtigung der
nichtparabolischen Korrektur ergibt sich aus der Ableitung der Energie
nach dem Wellenvektor der Faktor
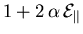 .
.
Die kinetische Energie bezieht sich auf das Energieminimum im Subband 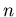
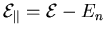 |
(2.76) |
(2.77) gibt die Zustandsdichte für ein
einzelnes Subband 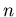 an. Der prinzipielle Verlauf der gesamten
Zustandsdichte unter Berücksichtigung mehrerer Subbänder ist in
Abbildung 2.6 skizziert. Im Fall der
nichtparabolischen Korrektur erhält man anstelle der konstanten Dichte
eine mit der Energie linear ansteigende Funktion. Der Verlauf der
nichtquantisierten Zustandsdichte ist durch die strichpunktierte Linie
angedeutet.
an. Der prinzipielle Verlauf der gesamten
Zustandsdichte unter Berücksichtigung mehrerer Subbänder ist in
Abbildung 2.6 skizziert. Im Fall der
nichtparabolischen Korrektur erhält man anstelle der konstanten Dichte
eine mit der Energie linear ansteigende Funktion. Der Verlauf der
nichtquantisierten Zustandsdichte ist durch die strichpunktierte Linie
angedeutet.
Abbildung 2.6:
Verlauf der Zustandsdichte im quantisierten Fall mit (rechts)
und ohne (links) nichtparabolische Korrektur.
|
|
Bei der Berechnung der Elektronenkonzentration im quantisierten Fall ist über
die diskreten Zustände zu
summieren und über die kontinuierlichen Zustände zu integrieren.
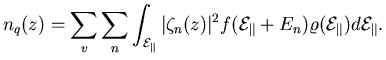 |
(2.77) |
In der Summation läuft der Index 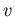 über alle Talsorten und der Index
über alle Talsorten und der Index
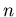 über alle Subbänder je Talsorte. Bei den Integrationsgrenzen muss
das in unserem Fall verwendete Energielimit als obere Schranke
berücksichtigt werden. Setzt man in (2.79)
die Fermi-Verteilung (2.70) ein und wertet die
Integration über die Energie sowohl im parabolischen als auch im
nichtparabolischen Fall aus so erhält man:
über alle Subbänder je Talsorte. Bei den Integrationsgrenzen muss
das in unserem Fall verwendete Energielimit als obere Schranke
berücksichtigt werden. Setzt man in (2.79)
die Fermi-Verteilung (2.70) ein und wertet die
Integration über die Energie sowohl im parabolischen als auch im
nichtparabolischen Fall aus so erhält man:
Zusätzlich zu den Größen (2.75) haben wir hier die von
den Eigenwerten
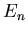 abhängigen Größen
abhängigen Größen 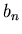 verwendet.
verwendet.
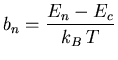 |
(2.80) |
Abbildung 2.7:
Zerlegung der Elektronenkonzentration in klassischen und
quantenmechanischen Anteil.
|
|
Abbildung 2.7 zeigt den quantenmechanisch und den
klassisch Berechneten Anteil an der Elektronenkonzentration im
Inversionskanal eines MOS-Transistors.
Abbildung 2.8:
Eindimensionale Diskretisierung mittels Boxintegration
und Definition von linksseitigem und rechtsseitigem Grenzwert.
|
|
Die Lösungen der Schrödinger-Gleichung (2.52)
liegen im Fourier-Bereich vor. Die Berechnung der Trägerkonzentration
nach (2.81) wird jedoch im Ortsraum durchgeführt.
Diese Trägerkonzentration ist über die einhüllenden Funktionen
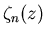 und den Verlauf der Bandkanten von der Koordinate
und den Verlauf der Bandkanten von der Koordinate 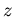 abhängig, und wird bei der Lösung der
Poisson-Gleichung (2.67) im Ortsraum verwendet. Mit
der Methode der Boxintegration erhalten wir eine Diskretisierung der
eindimensionalen Poisson-Gleichung, in der unstetige Größen wie die
Dielektrizitätskonstante berücksichtigt werden. Für einen Gitterpunkt
abhängig, und wird bei der Lösung der
Poisson-Gleichung (2.67) im Ortsraum verwendet. Mit
der Methode der Boxintegration erhalten wir eine Diskretisierung der
eindimensionalen Poisson-Gleichung, in der unstetige Größen wie die
Dielektrizitätskonstante berücksichtigt werden. Für einen Gitterpunkt
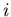 ergibt sich der folgende Zusammenhang für die Potenzialwerte der
Nachbarpunkte.
ergibt sich der folgende Zusammenhang für die Potenzialwerte der
Nachbarpunkte.
An allen Kontaktstellen zwischen zwei verschiedenen Materialien ist es
notwendig rechtsseitige (Index 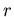 ) und linksseitige (Index
) und linksseitige (Index 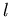 ) Werte
für die nicht kontinuierlichen Größen wie zum Beispiel der
Ladungsträgerkonzentration zu verwenden. Die Verhältnisse für einen
Gitterpunkt mit dem Index
) Werte
für die nicht kontinuierlichen Größen wie zum Beispiel der
Ladungsträgerkonzentration zu verwenden. Die Verhältnisse für einen
Gitterpunkt mit dem Index 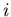 an dem die Größe
an dem die Größe 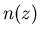 eine
Diskontinuität aufweist, sowie die verwendeten Boxen für die
Boxintegration sind in Abbildung 2.8
skizziert. Für jene Materialeigenschaften, die nicht auf den
Gitterpunkten definiert sind, also beispielsweise für die
Dielektrizitätskonstante
eine
Diskontinuität aufweist, sowie die verwendeten Boxen für die
Boxintegration sind in Abbildung 2.8
skizziert. Für jene Materialeigenschaften, die nicht auf den
Gitterpunkten definiert sind, also beispielsweise für die
Dielektrizitätskonstante
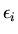 , beziehen sich die Indizes
, beziehen sich die Indizes 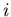 auf
jenen Wert, den der Parameter zwischen den Punkten
auf
jenen Wert, den der Parameter zwischen den Punkten 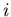 und
und 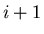 hat.
Die Lösung der diskreten Gleichung (2.83) wird über
eine Newton-Iteration bewerkstelligt.
hat.
Die Lösung der diskreten Gleichung (2.83) wird über
eine Newton-Iteration bewerkstelligt.
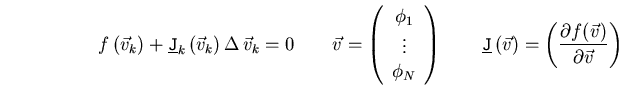 |
|
|
(2.82) |
Dazu muss in jedem Schritt 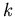 das Residuum
das Residuum
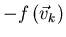 und die Jakobi-Matrix
und die Jakobi-Matrix
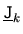 ausgewertet werden.
Wenn wir als Randbedingung die
Potenzialwerte an den Bereichsgrenzen vorgeben, erhalten wir für die
Jakobi-Matrix folgende Bandmatrix.
ausgewertet werden.
Wenn wir als Randbedingung die
Potenzialwerte an den Bereichsgrenzen vorgeben, erhalten wir für die
Jakobi-Matrix folgende Bandmatrix.
Für die Löcherkonzentration ergibt sich bei Verwendung der Boltzmann-Statistik
folgende lokale Ableitung nach dem Potenzial.
Für den klassischen Beitrag zur Elektronenkonzentration ergibt sich bei
Verwendung der Fermi-Statistik folgende lokale Ableitung nach dem
Potenzial.
In der Jakobi-Matrix (2.85) wird die Ableitung des
quantenmechanischen Beitrags
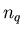 zur Elektronendichte nach dem
Potenzial benötigt. Da
zur Elektronendichte nach dem
Potenzial benötigt. Da
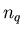 nach (2.81) aus den
Lösungen der Schrödinger-Gleichung berechnet wird, hängt dessen Wert
vom gesamten Verlauf des Potenzials ab. In einem ersten Ansatz kann
man die erforderliche lokale Ableitung im Rahmen einer
selbstkonsistenten Lösung durch Abspeichern der zuletzt berechneten
Elektronendichte aus der Differenz zum aktuellen Wert ermitteln. Der
in [46] vorgestellte Ansatz liefert eine genauere
Abschätzung für die Ableitung der Elektronendichte und soll hier kurz
wiedergegeben werden.
nach (2.81) aus den
Lösungen der Schrödinger-Gleichung berechnet wird, hängt dessen Wert
vom gesamten Verlauf des Potenzials ab. In einem ersten Ansatz kann
man die erforderliche lokale Ableitung im Rahmen einer
selbstkonsistenten Lösung durch Abspeichern der zuletzt berechneten
Elektronendichte aus der Differenz zum aktuellen Wert ermitteln. Der
in [46] vorgestellte Ansatz liefert eine genauere
Abschätzung für die Ableitung der Elektronendichte und soll hier kurz
wiedergegeben werden.
Die Elektronendichte läßt sich nach (2.81)
als eine Summe über alle Täler und Subbänder anschreiben, in der
jeweils das Produkt aus dem Quadrat der einhüllenden Funktionen
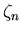 und der Besetzungswahrscheinlichkeit, hier durch die
Funktion
und der Besetzungswahrscheinlichkeit, hier durch die
Funktion 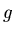 dargestellt, vorkommt.
dargestellt, vorkommt.
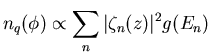 |
(2.86) |
Gesucht wird der Einfluß einer Veränderung des Potenzial
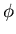 um
eine Srtörung
um
eine Srtörung
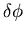 . Dieser Änderung im Potenzial entspricht
einer Störung des Hamilton-Operators
. Dieser Änderung im Potenzial entspricht
einer Störung des Hamilton-Operators
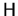 um einen Beitrag
um einen Beitrag
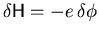 |
(2.87) |
Die daraus resultierende Änderung der Elektronendichte
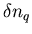 wollen wir in Form einer Linearisierung ermitteln. Durch die Störung
werden die in (2.88) verwendeten Eigenwerte und die
einhüllenden Funktionen verändert.
wollen wir in Form einer Linearisierung ermitteln. Durch die Störung
werden die in (2.88) verwendeten Eigenwerte und die
einhüllenden Funktionen verändert.
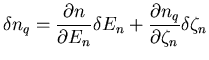 |
(2.88) |
Die beiden Beiträge zur veränderten Elektronendichte werden über
die Störungsrechnung ermittelt.
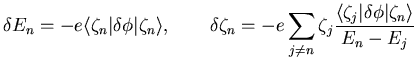 |
(2.89) |
Setzt man (2.91) in (2.90) ein
so erhält man:
Aus der Ableitung des Quadrats der Wellenfunktion ergibt sich ein
Faktor 2 in (2.93). Diesen kann man ausnutzen, um
die Summen in (2.93) zweimal
anzuschreiben. Vertauscht man im zweiten Term die Indizes 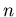 und
und 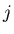 so erhält man wegen der Symmetrie der Matrixelemente:
so erhält man wegen der Symmetrie der Matrixelemente:
Verwendet man für die Differenz der Besetzungswahrscheinlichkeiten
die Näherung
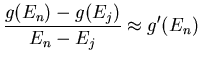 |
(2.93) |
so kommt in beiden Termen der Gleichung (2.91)
die Ableitung der Besetzungswahrscheinlichkeit vor.
Aus der Vollständigkeitsrelation (2.19) läßt sich
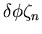 wie folgt anschreiben.
wie folgt anschreiben.
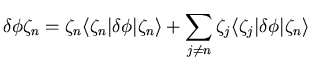 |
(2.94) |
Wir setzen nun (2.94)
und (2.92) in (2.91) ein und
berücksichtigen den Zusammenhang (2.96).
Es ergibt sich somit ein lokaler Zusammenhang zwischen der Änderung des
Potenzials und der daraus resultierenden Veränderung der
Elektronendichte. Die verwendete Näherung (2.95)
läßt sich bei starker Quantisierung,
und den dann auftretenden großen Energiedifferenzen zwischen den
Eigenwerten, nur durch die gute Konvergenz der selbskonsistenten
Lösung von Schrödinger- und Poisson-Gleichung rechtfertigen.
Wir wenden nun (2.97) auf die parabolische
Elektronenkonzentration (2.80) an.
Mit (2.98) sind nun alle Ableitungen
bekannt, die bei der Berechnung der
Jakobi-Matrix (2.85) benötigt werden.



Next: 2.5 Selbstkonsistente Lösung
Up: 2. Schrödinger-Poisson-Solver
Previous: 2.3 Erweiterung auf Heterostrukturen
C. Troger: Modellierung von Quantisierungseffekten in Feldeffekttransistoren
![]() .
Die Raumladungsdichte
.
Die Raumladungsdichte ![]() besteht aus mehreren Komponenten.
Für die Beschreibung der ortsfesten Ladungen im Simulationsgebiet
werden die Konzentration der Donatoren und
Akzeptoren,
besteht aus mehreren Komponenten.
Für die Beschreibung der ortsfesten Ladungen im Simulationsgebiet
werden die Konzentration der Donatoren und
Akzeptoren, ![]() und
und ![]() , verwendet.
, verwendet. ![]() steht für die
Löcherkonzentration.
Bei den Elektronen wird der Beitrag der nicht quantisiert betrachteten
Elektronen durch
steht für die
Löcherkonzentration.
Bei den Elektronen wird der Beitrag der nicht quantisiert betrachteten
Elektronen durch
![]() berücksichtigt.
Der Anteil
berücksichtigt.
Der Anteil
![]() der Elektronenkonzentration wird aus den
Lösungen der Schrödinger-Gleichung berechnet.
der Elektronenkonzentration wird aus den
Lösungen der Schrödinger-Gleichung berechnet.
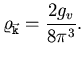
![]() wird die Fermi-Dirac-Statistik
verwendet. Unter Benutzung des Begriffs der Fermi-Energie
wird die Fermi-Dirac-Statistik
verwendet. Unter Benutzung des Begriffs der Fermi-Energie
![]() und
der Elektronentemperatur
und
der Elektronentemperatur
![]() , welche hier mit der Gittertemperatur
gleichgesetzt wird, lautet die Wahrscheinlichkeit für die Besetzung eines
Zustands mit der Energie
, welche hier mit der Gittertemperatur
gleichgesetzt wird, lautet die Wahrscheinlichkeit für die Besetzung eines
Zustands mit der Energie
![]()
![]() -Raum vorliegen.
Eine Umformung zwischen den beiden Darstellungen kann
über die Teilchenerhaltung erfolgen.
-Raum vorliegen.
Eine Umformung zwischen den beiden Darstellungen kann
über die Teilchenerhaltung erfolgen.
![]() an. Darin laufen
die beiden Winkel
an. Darin laufen
die beiden Winkel ![]() und
und ![]() von 0 bis
von 0 bis ![]() beziehungsweise von 0 bis
beziehungsweise von 0 bis ![]() . Bei Verwendung der parabolischen
Dispersionsrelation (2.33) ergibt sich durch
Einsetzen in (2.71) die bekannte Formel
. Bei Verwendung der parabolischen
Dispersionsrelation (2.33) ergibt sich durch
Einsetzen in (2.71) die bekannte Formel
![]() beginnen soll. Auf diese Weise setzt sich die Elektronenkonzentration aus
zwei Beiträgen zusammen, dem klassischen Anteil
beginnen soll. Auf diese Weise setzt sich die Elektronenkonzentration aus
zwei Beiträgen zusammen, dem klassischen Anteil
![]() und
einem Anteil
und
einem Anteil
![]() , der aus der Lösung der Schrödinger-Gleichung
berechnet wird.
, der aus der Lösung der Schrödinger-Gleichung
berechnet wird.
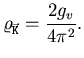
![]() an. Der prinzipielle Verlauf der gesamten
Zustandsdichte unter Berücksichtigung mehrerer Subbänder ist in
Abbildung 2.6 skizziert. Im Fall der
nichtparabolischen Korrektur erhält man anstelle der konstanten Dichte
eine mit der Energie linear ansteigende Funktion. Der Verlauf der
nichtquantisierten Zustandsdichte ist durch die strichpunktierte Linie
angedeutet.
an. Der prinzipielle Verlauf der gesamten
Zustandsdichte unter Berücksichtigung mehrerer Subbänder ist in
Abbildung 2.6 skizziert. Im Fall der
nichtparabolischen Korrektur erhält man anstelle der konstanten Dichte
eine mit der Energie linear ansteigende Funktion. Der Verlauf der
nichtquantisierten Zustandsdichte ist durch die strichpunktierte Linie
angedeutet.
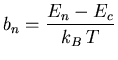
![\includegraphics[]{Schroedinger/PoissonBox-fin.eps}](img406.png)
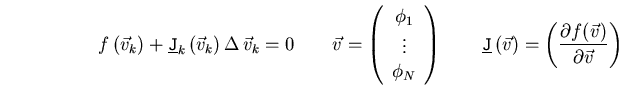
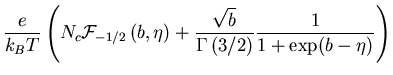
![]() zur Elektronendichte nach dem
Potenzial benötigt. Da
zur Elektronendichte nach dem
Potenzial benötigt. Da
![]() nach (2.81) aus den
Lösungen der Schrödinger-Gleichung berechnet wird, hängt dessen Wert
vom gesamten Verlauf des Potenzials ab. In einem ersten Ansatz kann
man die erforderliche lokale Ableitung im Rahmen einer
selbstkonsistenten Lösung durch Abspeichern der zuletzt berechneten
Elektronendichte aus der Differenz zum aktuellen Wert ermitteln. Der
in [46] vorgestellte Ansatz liefert eine genauere
Abschätzung für die Ableitung der Elektronendichte und soll hier kurz
wiedergegeben werden.
nach (2.81) aus den
Lösungen der Schrödinger-Gleichung berechnet wird, hängt dessen Wert
vom gesamten Verlauf des Potenzials ab. In einem ersten Ansatz kann
man die erforderliche lokale Ableitung im Rahmen einer
selbstkonsistenten Lösung durch Abspeichern der zuletzt berechneten
Elektronendichte aus der Differenz zum aktuellen Wert ermitteln. Der
in [46] vorgestellte Ansatz liefert eine genauere
Abschätzung für die Ableitung der Elektronendichte und soll hier kurz
wiedergegeben werden.
![]() und der Besetzungswahrscheinlichkeit, hier durch die
Funktion
und der Besetzungswahrscheinlichkeit, hier durch die
Funktion ![]() dargestellt, vorkommt.
dargestellt, vorkommt.