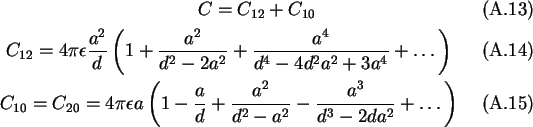Next: A.4 Capacitance of an
Up: A Capacitance Calculations
Previous: A.2 Self Capacitance of
First we study the case of a point charge near a grounded
conducting sphere by the image charge method.
Removing the conductor we try
to find the position and magnitude of an `image' charge q', as in
Fig. A.2, that will make the potential zero on the spherical
surface.
Figure:
A point charge q at a distance d from the center of a
grounded conducting sphere of radius a. The boundary condition
 on the spherical surface is satisfied by the original
charge q and its image q'.
on the spherical surface is satisfied by the original
charge q and its image q'.
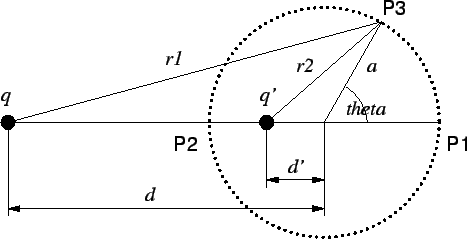 |
It is clear from the symmetry of the problem, that if such a charge exists
it must lie on the line connecting q and the center of the sphere.
We begin by forcing the potential to vanish at the points P
 and
P
and
P
 .
Then
.
Then
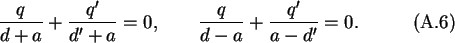
Solving these two equations gives
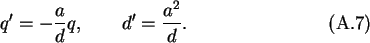
We still have to assure whether this charge arrangement will make the
potential zero at a general point P
 on the surface of the sphere.
At P
on the surface of the sphere.
At P
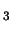

where
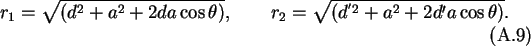
Taking q' and d' as in (A.7) does in fact make
 at P
at P
 ,
as required. Since this set of charges has a
rotation symmetry around the axis P
,
as required. Since this set of charges has a
rotation symmetry around the axis P
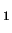 -P
-P
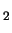 ,
the
condition is indeed fulfilled for all points on the sphere.
,
the
condition is indeed fulfilled for all points on the sphere.
Applying the above result for a successive approximation in a method of
images, one can calculate the capacitance of two spheres, which is applied
here for two equal spheres. We are
replacing both spheres by a set of point charges which will maintain the
conductor surfaces as equipotentials.
First we put a charge q at the center of the left sphere, as in
Fig. A.3.
Figure A.3:
Two conducting spheres at distance d and with radius a. One sphere
is connected to ground.
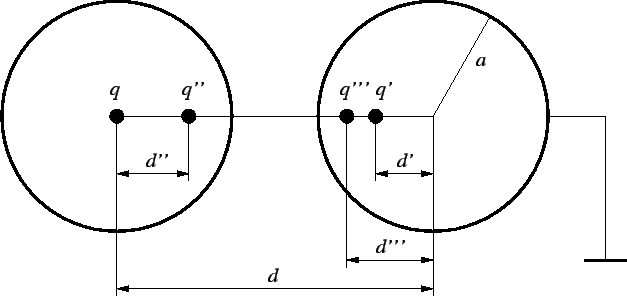 |
This makes the left sphere an equipotential, but not the right sphere. Next
we put the `image' charge q' in the right sphere. This makes the right
sphere a zero equipotential but destroys the spherical potential on the left.
So we put the `image' of the `image' q'' inside the left sphere, to
compensate for q'. This makes the left sphere again an equipotential but
upsets the right sphere. We continue the process which converges rapidly,
until we reach the required precision.
The total charge on the left sphere is
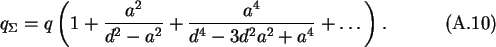
But only q contributes to its potential. The charges q' and q'' cause
the potential, they contribute to the left sphere, to vanish, and the same is
true of all following pairs of charges. The potential of the left sphere is
therefore

The charges q and q' have a zero contribution to the potential of the
right sphere and so do the pairs q'', q''' a.s.o.
Since the potential of the right sphere was always compensated to zero the
total capacitance of either sphere is
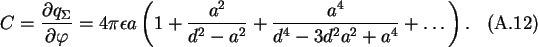
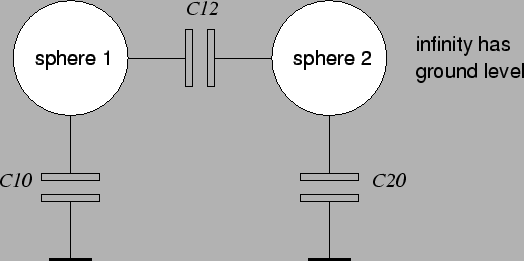
The total capacitance C can be split in a capacitance between the spheres
C12 and a capacitance to infinity or self-capacitance of the
sphere C10, as shown in
Fig. A.4.
Table A.1:
Charges and location of successive compensation charges.
| left sphere |
right sphere |
| |
| charge | distance | charge | distance |
| | from center | | from center |
| | | | |
| q | 0 |
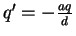 |
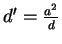 |
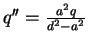 |
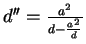 |
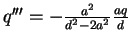 |
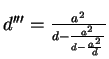 |
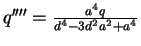 |
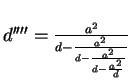 |
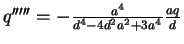 |
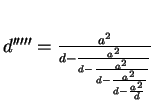 |
|
Figure A.4:
Two conducting spheres and their capacitances.
 |
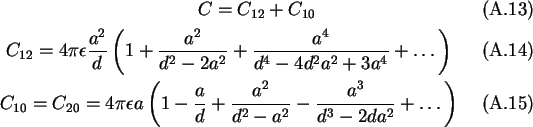




Next: A.4 Capacitance of an
Up: A Capacitance Calculations
Previous: A.2 Self Capacitance of
Christoph Wasshuber


![]() and
P
and
P
![]() .
Then
.
Then
![]()
![]()
![]() on the surface of the sphere.
At P
on the surface of the sphere.
At P
![]()
![]()
![]()
![]() at P
at P
![]() ,
as required. Since this set of charges has a
rotation symmetry around the axis P
,
as required. Since this set of charges has a
rotation symmetry around the axis P
![]() -P
-P
![]() ,
the
condition is indeed fulfilled for all points on the sphere.
,
the
condition is indeed fulfilled for all points on the sphere.