9.2 An In-Segregation Model in One and Two Dimensions

Next: 9.3 A Novel Diffusion Up: 9. Examples Previous: 9.1 A Pair-Diffusion Model

9.2 An In-Segregation Model in One and Two Dimensions

Another very important effect occurring during device fabrication is the phenomenon of segregation [13] [14]. The standard treatment to simulate this effect is to split a simulation domain into two different homogeneous regions separated by an abrupt interface. The most common formulation to handle this problem is by describing it as a segregation flux across the interface

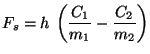$\displaystyle F_s = h \: \left(\frac{C_1}{m_1}-\frac{C_2}{m_2}\right)$

(11)

where

represents the mass transfer coefficient,

and

the concentrations in the separated areas and

the equilibrium segregation.

In some cases the separation into two different homogeneous regions is not treatable or leads to unacceptable errors. Therefore we tried to use the diffusion-segregation equation developed by Tan et al. [15] to solve a segregation effect with one single domain using a parameter dependent small transition zone to simulate the interface. The example can be described by the following equations

$\displaystyle \frac{\partial C}{\partial t} = div\: \left[ D\: \left( grad\left( C\right) -\frac{C}{m}\: grad\left( m\right) \right) \right]$

(12)

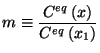$\displaystyle m\equiv \frac{C^{eq}\left( x\right) }{C^{eq}\left( x_{1}\right) }$

(13)

where $C^{eq}\left( x_1\right)$ is the species' solubility at an arbitrarily chosen reference point 1.

**Figure 12:** Dopant distribution in an inhomogeneous material
$\resizebox{13.0cm}{!}{\includegraphics{eps/seg1d.eps}}$

Fig. 12 shows an in-diffusion-segregation profile of a species in a crystal consisting of three heterostructures where the first and the third area are of the same material. The conditions for the transmission zone at the interface are specified in a way so that the change of the materials takes place within one element. The smaller the element, the better are the numerical results in comparison to a sharp interface formulation.

**Figure 13:** Segregation effect calculated with an adaptive grid to account for a circular inhomogeneity
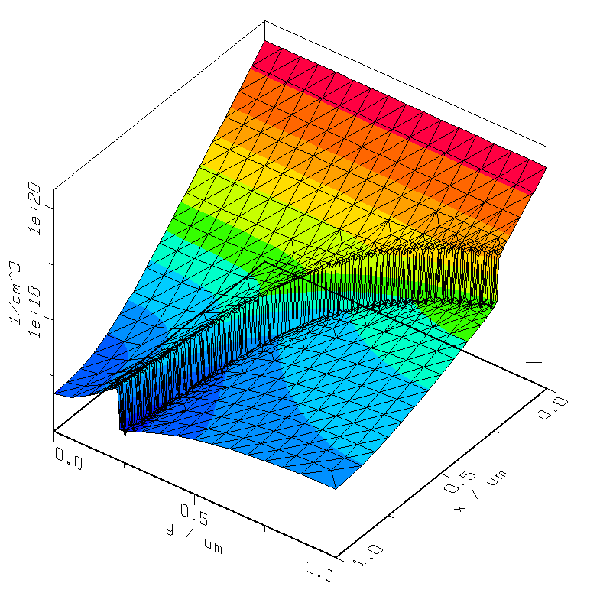
$\resizebox{13.0cm}{!}{\includegraphics{eps/seg2d.eps}}$

The two-dimensional simulation result (Fig. 13) shows the advantage of an in-segregation model in case of non-planar geometries. It is rather complicated with respect to the necessary meshing algorithm to split this geometry into two separated regions whereas it is comparable easy to solve the in-segregation along the given interface. As boundary condition a Dirichlet boundary with a concentration of $C=10^{20} cm^{-3}$ has been chosen on the top edge. All other boundaries are natural reflecting. The inhomogeneity within the simulation domain is circular. The result shows that the diffusing species are blocked at the boundary due to the material interface. To increase the accuracy a grid criterion has been defined which adapts the interface between the two materials. To minimize the numerical error at the interface the same conditions for the transition zone as in the one-dimensional case have been chosen.

Next: 9.3 A Novel Diffusion Up: 9. Examples Previous: 9.1 A Pair-Diffusion Model

M. Radi, E.Leitner, and S. Selberherr