next up previous
Next: 9.4 Three-Dimensional Temperature Distribution Up: 9. Examples Previous: 9.2 An In-Segregation Model

9.3 A Novel Diffusion Coupled Oxidation Model in Three Dimensions

To describe local oxidation, a model with a smooth transition zone between silicon and silicon dioxide is assumed[16].

Figure 14: Domain and boundary settings
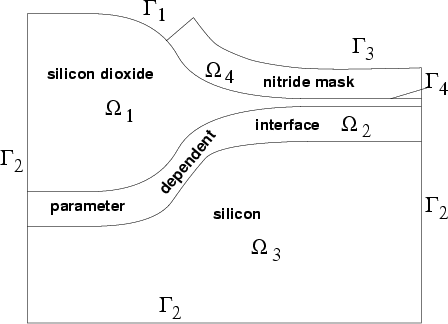
\begin{figure} \centering\epsfig{file=eps/domain.eps,width=1.0\textwidth} \end{figure}

For the definition of the model consider figure [14] as computation domain $ \Omega$ which consists of a pure silicon dioxide range $ \Omega_1$, an interface range $ \Omega_2$ with a mixture of silicon and silicon dioxide, a pure silicon range $ \Omega_3$ and a nitride mask $ \Omega_4$ which is defined on a mesh of its own and is connected to $ \Omega_1$ via boundary $ \Gamma_4$ to transmit mechanical displacements. For the nitride mask an elastic model is used to calculate its stress-strain contribution. To describe the different phases of oxygen within the domain $ \Omega_1~\cup~\Omega_2~\cup~\Omega_3$ a generation/recombination ratio of oxygen

$\displaystyle R_O=k_{r}\: \left(1-\eta(x,t)\right) \: C_{O}$     (14)

is defined, where $ \eta=f\left(\frac{C_{SiO_2}\left(x,t\right)}{C_{Si_0}}\right)$ is a function of a normalized silicon dioxide concentration related to the $ C_{Si_0}$ concentration of silicon in pure crystal. $ \eta$ varies between one (pure silicon dioxide) and zero (pure silicon).

The generation of silicon dioxide itself is handled by the formulation

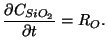$\displaystyle \frac{\partial C_{SiO_2}}{\partial t} = R_O.$     (15)

The free oxidant diffusion is described by a nonlinear partial diffusion equation which determines the growth of the concentration of generated silicon dioxide and therefore the growth-rate of the oxide at the material interface
$\displaystyle \frac{\partial C_{O}}{\partial t}=div\left[D(\left(\eta(x,t)\right)\cdot grad\left( C_{O}\right) \right] - 2\cdot R_O.$     (16)

For the volumetric expansion we solve the equilibrium condition

$\displaystyle \left(\int\limits_V{{\cal L^T}\cdot{\cal D}\left(\eta(x,t)\right)... ...ts_V{{\cal L^T}\cdot{\cal D}\left(\eta(x,t)\right)\cdot\{\epsilon_o\}}\cdot\:dV$     (17)

where u, $ \epsilon_o$, $ \cal L$ and $ \cal D$ represents the displacement vector, the strain caused by silicon dioxide generation, the mechanical operator defined as $ \{\epsilon\}={\cal L}\cdot\{u\}$ and the elasticity matrix, respectively. The right hand side of (17) can be interpreted as an energy term caused by the chemical reaction between silicon and silicon-dioxide. Finally, the volume dilatation within the oxide is calculated by a hydrostatic pressure term


$\displaystyle p=-\chi \cdot (\epsilon_{xx} + \epsilon_{yy} + \epsilon_{zz}) \quad \Longrightarrow \quad \Delta V$     (18)

As an example two typical three-dimensional effects arising in the corners of the nitride mask have been investigated (Fig. 15). Starting from a pure silicon block the results show, that the introduced model can even handle structures without pad oxide below the nitride mask, which leads to the effect, that the interface meets the nitride layer vertically, which can hardly be solved by algorithms based on a sharp interface formulation.

Figure 15: Oxidation of typical three-dimensional effects arising in the corners of the nitride mask
\includegraphics[width=8.0cm]{eps/erg1.eps}
\includegraphics[width=8.0cm]{eps/erg2.eps}

next up previous
Next: 9.4 Three-Dimensional Temperature Distribution Up: 9. Examples Previous: 9.2 An In-Segregation Model
M. Radi, E.Leitner, and S. Selberherr