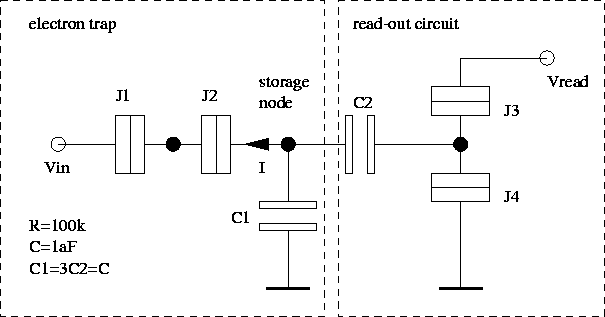
Figure 6: Electron trap with read-out circuit.
An electron trap with a read-out circuit as shown in Fig. 6 is simulated.

A voltage pulse on Vin transports one elementary charge onto the
'storage node'. This stored charge influences via C2 the read-out
circuit which is a single-electron transistor. The current through the
read-out transistor depends on the charge which is stored in the trap.
We are interested in the leakage current I or which is equivalent, in
the lifetime of a stored electron. The lifetime t and leakage current
are related by
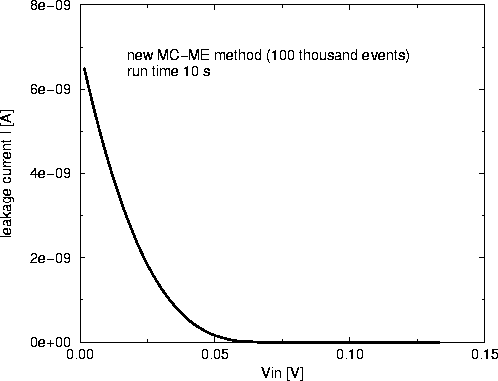
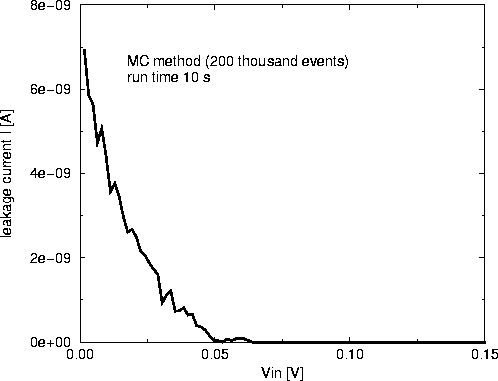
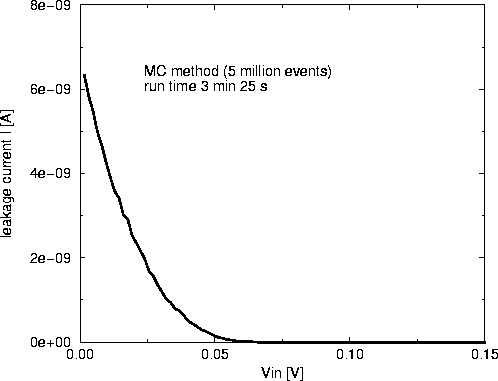
It can be clearly seen form Fig. 7, that our new MC-ME algorithm produces in a short simulation time much better results than the plain MC method (Fig. 8). One has to simulate with a plain MC method many more tunnel events to achieve a similar accuracy (Fig. 9). The reason for this is that the read-out circuit consumes many tunnel events which do not contribute to the accuracy of the leakage current. In bigger and more complicated circuits this problem can be much more pronounced and render a plain MC method useless for co-tunneling simulations.