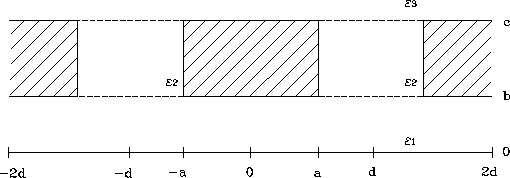
Abbildung 7.1: Leiter über Erdungsfläche




Die in [Che92][Wri93][Sak83][Yua82] angegebenen Formen, welche Kapazitäten einer oder mehrere Leiterbahnen über einer Erdungsfläche berechnen, werden meist durch einfache Polynome gebildet, die außerdem nur in einem ganz bestimmten und meist stark eingeschränkten Definitionsbereich Lösungen mit ausreichender Genauigkeit liefern. Diese Formeln werden meist durch Parametervariation an die Lösungen numerischer Berechnungen angepaßt.
Es es jedoch möglich, wie in [Rin93] gezeigt wird, eine analytische Lösung für einen geraden rechteckigen Leiter über einer Erdungsfläche anzugeben. In [Rin93] wird die Laplace-Gleichung durch einen Separationsansatz in zwei Differentialgleichungen aufgeteilt. In vertikaler Richtung wird ein exponentieller Abfall angesetzt und in horizontaler Richtung fordert man eine periodische Fortsetzung der Struktur. Die geometrische Struktur erfordert eine Zerlegung des Isolatorgebiets in drei horizontale Teilgebiete, wobei Rand- bzw. Stetigkeitsbedingungen an den Grenzflächen zu erfüllen sind.
Die Lösung des Problems mit drei verschiedenen [Rin93] Materialien kann mit einem symbolischen Mathematikprogramm in einigen Minuten gefunden werden. Für die unten angegebene Formulierung sind die in Abbildung 7.1 angegebenen Parameter zur Geometriespezifikation notwendig.

Abbildung 7.1: Leiter über Erdungsfläche
Die Variable  gibt die gewünschte Anzahl der Fourier-Koeffizienten
gibt die gewünschte Anzahl der Fourier-Koeffizienten
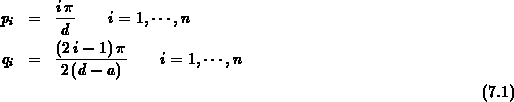
an. Die angegebene Lösung in aufbereiteter Form und in Matrizenschreibweise
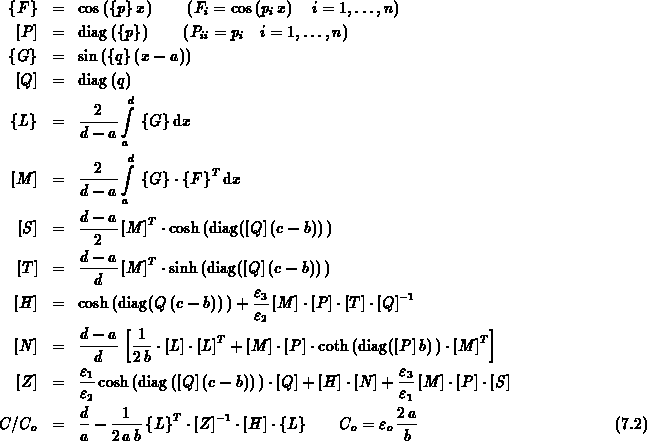
kann einfach an die Syntax eines verfügbaren Mathematikprogramms angepaßt werden.
 Für die weiteren Tests sollen die Strukturabmessungen
Für die weiteren Tests sollen die Strukturabmessungen 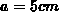 ,
, 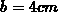 und
und 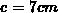 und
als Material Vakuum herangezogen werden. Der Matrixrang, welcher über die Anzahl der
Fourier-Koeffizienten
und
als Material Vakuum herangezogen werden. Der Matrixrang, welcher über die Anzahl der
Fourier-Koeffizienten  bestimmt ist, und der
Abstand der Spiegelungsebene
bestimmt ist, und der
Abstand der Spiegelungsebene 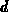 mit ihren homogene Neumann Randbedingungen als linke und
rechte Begrenzung sind noch frei wählbar.
Man kann die Ladungsdichte an der Oberfläche der Erdungsfläche am Punkt
mit ihren homogene Neumann Randbedingungen als linke und
rechte Begrenzung sind noch frei wählbar.
Man kann die Ladungsdichte an der Oberfläche der Erdungsfläche am Punkt 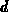 heranziehen und diese Ladungsdichte zur Ladungsdichte am Punkt 0 in der Mitte der
Anordnung setzen, um eine Fehlerabschätzung zu erhalten.
heranziehen und diese Ladungsdichte zur Ladungsdichte am Punkt 0 in der Mitte der
Anordnung setzen, um eine Fehlerabschätzung zu erhalten.
Wie sich aber im folgenden
zeigt, ist eine einfache zweidimensionale Parametervariation ausreichend, um ein Ergebnis
unter 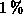 Genauigkeit zu erreichen.
Genauigkeit zu erreichen.
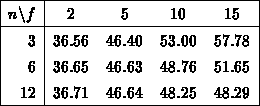
Die oberen Spalteneinträge f geben das Verhältnis 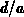 an. Alle berechneten Werte der Tabelle sind in
an. Alle berechneten Werte der Tabelle sind in
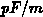 angegeben.
Der Wert der Kapazität mit
angegeben.
Der Wert der Kapazität mit 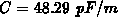 aus der Matrix in Zeile 3 und Spalte 4 ist,
spekulativ gesehen, genau genug, um damit numerische Berechnungen zu vergleichen.
aus der Matrix in Zeile 3 und Spalte 4 ist,
spekulativ gesehen, genau genug, um damit numerische Berechnungen zu vergleichen.
Die Abbildungen 7.2 und 7.3 zeigen die gleiche Konfiguration,
jedoch mit zwei verschiedenen Umrandungen: 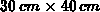 und
und 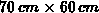 .
.
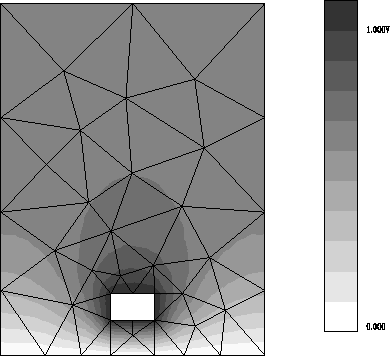
Abbildung 7.2: Leiter über Erdungsfläche, stark verzerrte Isolinien
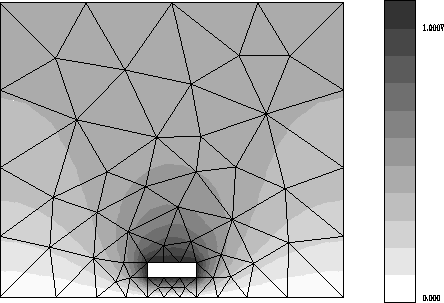
Abbildung 7.3: Leiter über Erdungsfläche, ausreichend große Umrandung
An dem gekrümmten Verlauf der Isolinien zum linken und rechten Rand kann man im ersten
Bild erkennen, daß das Diskretisierungsgitter zu klein ist.
Die folgende Tabelle gibt darüber Aufschluß, daß die zu kleinen Werte
in der zweiten Spalte kein Problem der Elementszahl sind, da die Elementszahl durch einen
Verfeinerungsschritt vervierfacht ( 4) bzw. durch einen zweiten Verfeinerungsschritt
um einen Faktor sechszehn (
4) bzw. durch einen zweiten Verfeinerungsschritt
um einen Faktor sechszehn ( 16) vergrößert wurde,
sondern explizit ein Problem der umschlossenen elektrostatischen Energie ist.
In einem Verfeinerungsschritt wird jedes Dreieck in vier ähnliche Unterdreiecke
zerlegt.
16) vergrößert wurde,
sondern explizit ein Problem der umschlossenen elektrostatischen Energie ist.
In einem Verfeinerungsschritt wird jedes Dreieck in vier ähnliche Unterdreiecke
zerlegt.
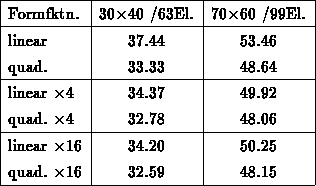
Wie in Abbildung 7.3 und in der
Tabelle gezeigt wird, kann man auch bei geringer Elementszahl eine Differenz zur vorhin
gezeigten Lösung durch Fourier-Reihenentwicklung kleiner als 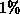 angeben.
angeben.
Es sollte damit gezeigt werden, daß man bei Problemstellungen, die ein nahezu
offenes Feldproblem darstellen,
das Diskretisierungsgitter ausreichend groß wählen muß
und der Anzahl der Elemente in diesem Fall eine untergeordnete Rolle zukommt,
da die elektrostatische Feldenergie über eine relativ große
Fläche verteilt ist.
Die letzte Spalte der Tabelle zeigt, daß eine Berechnung, die quadratische Formfunktionen und 99 Elemente
benutzt, ein genaueres Ergebnis liefert als 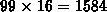 Elemente und lineare Formfunktionen.
Elemente und lineare Formfunktionen.
Die starke Verzerrungen der Äquipotentiallinien, bei einem relativ hohen Gradienten am linken und rechten Rand in der Abbildung 7.3, sind ein Zeichen dafür, daß das Ergebnis eine unzureichende Genauigkeit aufweisen wird.



