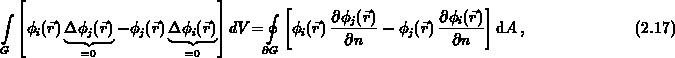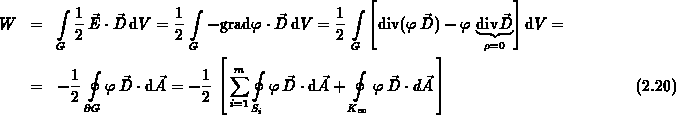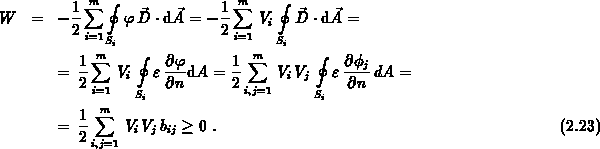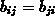 .
.Wendet man auf 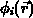 und
und 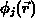 die 2. Greensche Formel an,
so gilt
die 2. Greensche Formel an,
so gilt
wobei 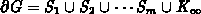 beschreibt.
beschreibt.
Mit (2.9) und (2.10) vereinfacht sich die Gleichung (2.17) auf
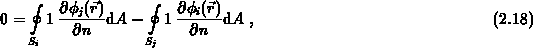
und es folgt mit (2.5): 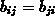 .
.
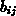 Matrix verschwindet nicht.
Matrix verschwindet nicht.
Nach Gleichung (2.8) gilt

und wegen der Symmetrie können auch die Spaltensummen nicht verschwinden.
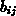 -Matrix ist positiv definit.
-Matrix ist positiv definit.Die elektrostatische Feldenergie ist, falls sich die Leiter auf beliebigen Potentialen befinden, mit
bestimmt. Um das Hüllenintegral über 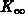 zu berechnen, werden die Gleichungen
(2.6) und (2.7) herangezogen
zu berechnen, werden die Gleichungen
(2.6) und (2.7) herangezogen
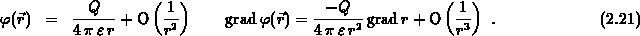
Damit erhält man für den Grenzwert des Hüllenintegrals:
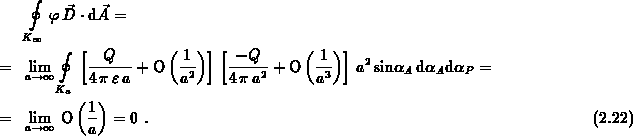
Den verbleibenden Energieterm aus Gleichung (2.20) unterzieht man einer weiteren Umformung:
Das Gleichheitszeichen in Gleichung (2.23) gilt für den Fall 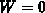 , woraus zunächst folgt,
daß
, woraus zunächst folgt,
daß 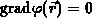 in
in 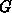 und
und 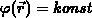 in
in 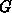 ist.
Nach (2.13) und (2.16) folgt
ist.
Nach (2.13) und (2.16) folgt 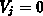 für
für 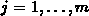 , das heißt, die Matrix der
Kapazitätskoeffizienten ist positiv definit.
, das heißt, die Matrix der
Kapazitätskoeffizienten ist positiv definit.