Um eine Diskretisierung durchführen zu können, muß eine Formulierung als
Extremwertaufgabe gefunden oder durch einen Galerkin-Ansatz
herbeigeführt werden.
Für die elliptische Differentialgleichung
gibt es eine äquivalente integrale Formulierung
wobei jene Funktion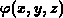 
eine Lösung ist, für welche ein Minimum des Integrals
unter Berücksichtigung der Dirichletschen Randbedingungen erreicht wird.
Das quadratische Funktional (3.2), welches eine eindeutige Lösung besitzt, läßt sich auch als
darstellen, was, wie leicht ersichtlich ist, der doppelten elektrostatischen Feldenergie
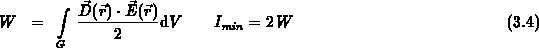
entspricht. Da die Aufgabenstellung die Behandlung verschiedener Materialien verlangt,
die Materialwerte aber als stückweise konstant angenommen werden können, ist
die Dielektrizitätszahl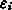 
im Segment 
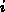ortsunabhängig. Damit
kann die Dielektrizitätszahl 
vor das Integral
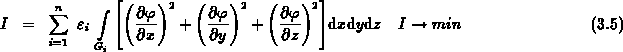
geschrieben werden.
