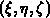 zum globalen
zum globalen
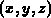 Koordinatensystem.
Koordinatensystem.




Die folgende Abbildungsvorschrift eines Tetraeders (Abbildung 3.1) beschreibt
den Übergang von dem lokalen Elementskoordinatensystem 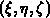 zum globalen
zum globalen
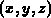 Koordinatensystem.
Koordinatensystem.
In Matrixform gilt

oder
mit der Jakobi-Matrix
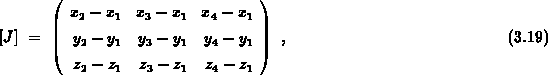
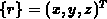 und
und 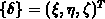 . Die Transformationsvorschrift
. Die Transformationsvorschrift  ist keine Funktion der lokalen Koordinaten
ist keine Funktion der lokalen Koordinaten 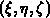 .
.
Nach Anwendung der Kettenregel (3.15) auf das Variationsintegral (3.2),
um auf die lokalen Koordinaten überzugehen, bleiben zunächst partielle Ableitungen
nach  ,
, 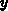 und
und  stehen. Diese Ableitungen
können durch die Knotenkoordinaten folgendermaßen eliminiert werden. Zunächst bildet
man von der Abbildungsvorschrift (3.16) die Ableitungen nach
stehen. Diese Ableitungen
können durch die Knotenkoordinaten folgendermaßen eliminiert werden. Zunächst bildet
man von der Abbildungsvorschrift (3.16) die Ableitungen nach 
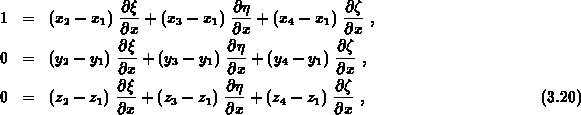
nach 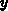
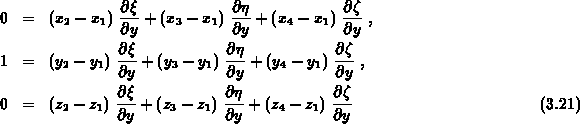
und nach 
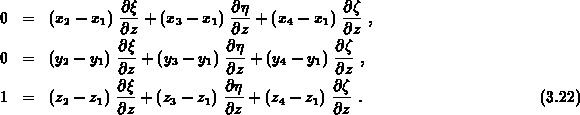
In Matrixnotation

ist die gesuchte Abhängigkeit mit
gefunden.