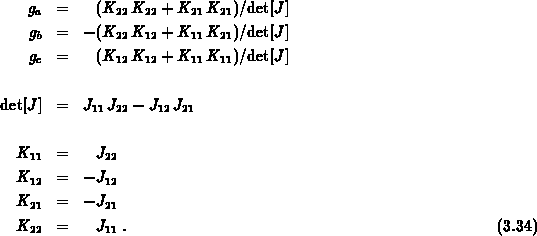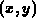 und lokalen Koordinaten
und lokalen Koordinaten 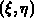 vereinfachen die Jakobi-Matrix zu
vereinfachen die Jakobi-Matrix zu




Die Transformation des Variationsintegrals (3.2) für ein Dreieck mit geraden
Kanten erfolgt in analoger Weise wie für den Tetraeder.
Die auf zwei Dimensionen reduzierten
globalen
Koordinaten 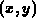 und lokalen Koordinaten
und lokalen Koordinaten 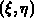 vereinfachen die Jakobi-Matrix zu
vereinfachen die Jakobi-Matrix zu

Dabei sind die drei Eckpunktsknoten des Elements gegen den Uhrzeigersinn numeriert.
Als Ergebnis erhält man ein Integral in den normierten Dreieckskoordinaten 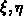
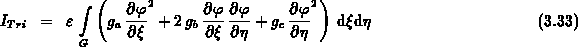
mit den neuen Koeffizienten