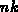Aufgrund der in Abschnitt 3.10.2 gewonnenen Erkenntnisse sind die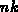 
Spalten
linear abhängig (siehe auch Gleichung (3.64)). Das bedeutet für das
Gleichungssystem, daß es ohne Vorgabe von Funktionswerten nicht invertierbar ist, da
gilt.
Die zur Matrix 
gehörende Form ist semidefinit.
Unter der Bedingung, daß nur ein einziger Funktionswert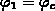 
festgelegt wird,
wodurch aber keine Beschränkung der Allgemeinheit gegeben ist [Haa92]),
ist die zu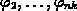 
gehörende quadratische Form positiv definit.
Die Behauptung läßt sich dadurch beweisen, daß der Term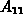 
aus dem Funktional
mit Hilfe von (3.64) eliminiert wird.
Für die reduzierte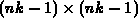 
große Matrix gilt nach (3.66)
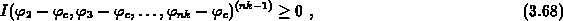
wobei null nur 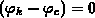für 
für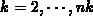 
angenommen wird.
Damit ist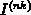 
positiv definit, und die Steifigkeitsmatrix bei assemblierten
Randbedingungen positiv definit.
