 eine
M-Matrix ist.
eine
M-Matrix ist. Da Dreieckselemente mit linearen Formfunktionen einfache geometrische Deutungen
zulassen, soll geklärt werden, unter welchen Umständen ein Nebendiagonaleintrag
Da Dreieckselemente mit linearen Formfunktionen einfache geometrische Deutungen
zulassen, soll geklärt werden, unter welchen Umständen ein Nebendiagonaleintrag
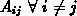 negativ ist.
negativ ist.




Nun soll geklärt werden, unter welchen Umständen die Matrix  eine
M-Matrix ist.
eine
M-Matrix ist. Da Dreieckselemente mit linearen Formfunktionen einfache geometrische Deutungen
zulassen, soll geklärt werden, unter welchen Umständen ein Nebendiagonaleintrag
Da Dreieckselemente mit linearen Formfunktionen einfache geometrische Deutungen
zulassen, soll geklärt werden, unter welchen Umständen ein Nebendiagonaleintrag
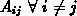 negativ ist.
negativ ist.
Die Variationsformulierung des Laplace-Operators in Dreieckskoordinaten 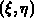
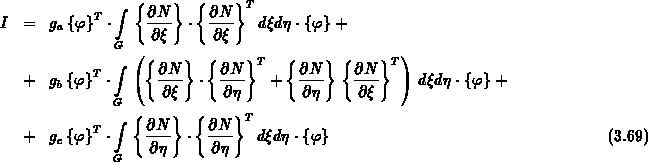
mit den linearen Formfunktionen
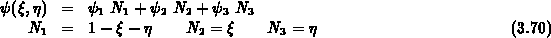
ergibt die folgenden drei Matrizen
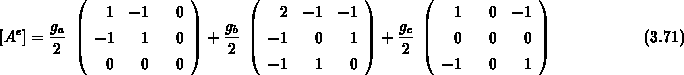
und deren geometrische Koeffizienten
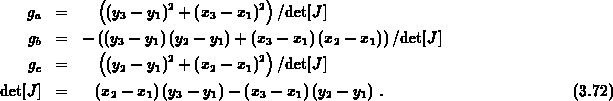
Zur Vereinfachung der Darstellung sollen die auch in Abbildung 3.13 gezeigten
Dreieckskanten mit 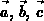 bezeichnet werden.
Die Terme
bezeichnet werden.
Die Terme 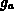 und
und 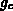 sind die quadrierten Dreieckskantenlängen
sind die quadrierten Dreieckskantenlängen 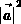 und
und 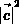 .
.
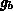 wird durch die gemischten partiellen Ableitungen gebildet und ist
als
wird durch die gemischten partiellen Ableitungen gebildet und ist
als 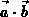 darstellbar.
Die drei Terme
darstellbar.
Die drei Terme 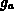 ,
, 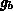 und
und 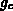 haben einen Gewichtungsfaktor gemeinsam, der durch die
zweifache Dreiecksfläche
haben einen Gewichtungsfaktor gemeinsam, der durch die
zweifache Dreiecksfläche 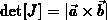 bestimmt wird. Da eine
Knotennumerierung gegen den Uhrzeigersinn vorausgesetzt wird, ist das äußere Produkt
bestimmt wird. Da eine
Knotennumerierung gegen den Uhrzeigersinn vorausgesetzt wird, ist das äußere Produkt
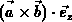 immer positiv.
immer positiv.
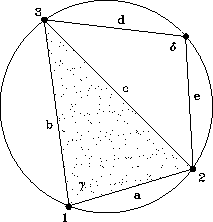
Abbildung 3.13: Delaunay-Kriterium
Aus diesen Überlegungen läßt sich ableiten, daß nur 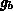 sein Vorzeichen wechseln kann.
sein Vorzeichen wechseln kann.
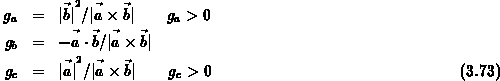
Um eine Aussage über die assemblierte Matrix zu machen, sind zunächst die Einträge der Elementsmatrix
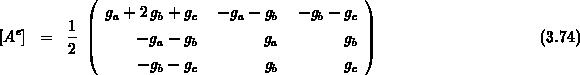
zu untersuchen. Bei den Diagonaleinträgen ist nur der erste Eintrag näher zu betrachten. Durch eine Umformung mit
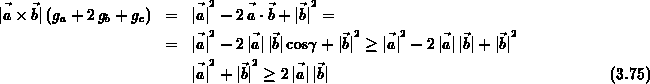
zeigt sich, daß dieser Eintrag immer positiv sein muß. Es gilt also allgemein:

Bei den Nebendiagonaleinträgen soll der ausgesuchte Term 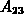 untersucht werden.
Die daraus gewonnene Schlüsse können verallgemeinert werden,
da bei gleicher Elementsanordnung und zyklischer Vertauschung der lokalen
Knotennumerierung eines Elements die Gesamtmatrix die gleichen Einträge
in geänderter Reihenfolge vorweisen muß.
untersucht werden.
Die daraus gewonnene Schlüsse können verallgemeinert werden,
da bei gleicher Elementsanordnung und zyklischer Vertauschung der lokalen
Knotennumerierung eines Elements die Gesamtmatrix die gleichen Einträge
in geänderter Reihenfolge vorweisen muß.
Der Eintrag 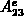 mit dem Koeffizienten
mit dem Koeffizienten 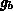 kann negativ oder positiv sein.
Den Matrixeintrag
kann negativ oder positiv sein.
Den Matrixeintrag 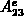
 bilden jedoch genau zwei Elemente: nämlich die beiden Elemente, die die Kante
bilden jedoch genau zwei Elemente: nämlich die beiden Elemente, die die Kante 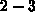 gemeinsam haben.
gemeinsam haben.
Abbildung 3.13 zeigt das Element 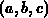 und das Nachbarelement
und das Nachbarelement 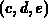 ,
wobei für eine M-Matrix die Summe beider Elementsanteile an der Stelle
,
wobei für eine M-Matrix die Summe beider Elementsanteile an der Stelle 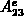 einen
negativen Gesamteintrag
einen
negativen Gesamteintrag

liefern muß.
Geht man von der vektoriellen Darstellung zu Beträgen und Winkelfunktionen mit

über, so erhält man eine Aussage über die erforderlichen Winkel in den beiden Dreiecken
als Ergebnis. Dieses Resultat entspricht den Forderungen einer Delaunay-Triangulierung
(siehe auch Abschnitt 5.1.1). Handelt es sich um ein Randelement, d.h. es gibt
kein Nachbarelement an der Kante 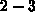 , so gilt
, so gilt 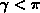 .
.
Gültig ist dieses Ergebnis aber nur dann, wenn beide Elemente das gleiche Material referenzieren. Allgemeiner gilt also

was zu der Schlußfolgerung führt:
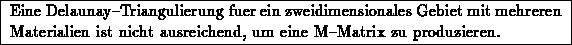
In drei Dimensionen konnte keine schlüssige Aussage über die Gesamtmatrix gemacht werden,
da die Koeffizienten  auch für die einfach gebauten Tetraederelemente durch die
Matrixinversion von
auch für die einfach gebauten Tetraederelemente durch die
Matrixinversion von 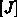 zu komplex werden. In [Let92] wird ein
Beispiel angegeben, das eine gültige Delaunay-Zerlegung darstellt, aber
dennoch keine M-Matrix ergibt.
zu komplex werden. In [Let92] wird ein
Beispiel angegeben, das eine gültige Delaunay-Zerlegung darstellt, aber
dennoch keine M-Matrix ergibt.
Es ist auch zu bemerken, daß bei der Anwendung von quadratischen Formfunktionen die
Matrix  keine M-Matrix ist, da schon die Elementsmatrizen positive und negative
Anteile enthalten und auch die Gesamtmatrix positive und negative Nebendiagonaleinträge
aufweist.
keine M-Matrix ist, da schon die Elementsmatrizen positive und negative
Anteile enthalten und auch die Gesamtmatrix positive und negative Nebendiagonaleinträge
aufweist.



