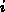 zusammenhängt. Dies geschieht
über einen symbolischen Assemblierungsvorgang, wobei z.B. nur die Indexmatrix
zusammenhängt. Dies geschieht
über einen symbolischen Assemblierungsvorgang, wobei z.B. nur die Indexmatrix 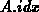 und
und
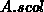 benötigt werden.
Danach werden die Einträge pro Zeile abgezählt, um die Anzahl der nächsten Nachbarn
benötigt werden.
Danach werden die Einträge pro Zeile abgezählt, um die Anzahl der nächsten Nachbarn
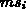 (Grad) zu bestimmen.
(Grad) zu bestimmen.




Der Cuthill-McKee-Algorithmus entspricht vom Aufbau her einer Baumstruktur (einem Graphen), wobei der Baum von der Wurzel ausgehend ebenenweise aufgebaut wird. Jeder neue Knoten wird nach den unten angegebenen Kriterien möglichst weit oben links in den Baum eingetragen.
Ausgangspunkt für die Erstellung einer neuen Knotennumerierung und damit der Baumstruktur
ist die Feststellung, mit wievielen Knoten ein Knoten 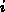 zusammenhängt. Dies geschieht
über einen symbolischen Assemblierungsvorgang, wobei z.B. nur die Indexmatrix
zusammenhängt. Dies geschieht
über einen symbolischen Assemblierungsvorgang, wobei z.B. nur die Indexmatrix 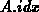 und
und
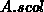 benötigt werden.
Danach werden die Einträge pro Zeile abgezählt, um die Anzahl der nächsten Nachbarn
benötigt werden.
Danach werden die Einträge pro Zeile abgezählt, um die Anzahl der nächsten Nachbarn
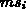 (Grad) zu bestimmen.
(Grad) zu bestimmen.
Als nächsten Schritt wählt man den Knoten mit dem geringsten Grad  als Startpunkt.
Bei mehreren Knoten mit minimalen Grad wird aus der minimalen Knotenmenge willkürlich ein
Knoten als Startpunkt gewählt.
Für das in Abbildung 4.3 gezeigte zweidimensionale Beispiel ist dies
eindeutig Knoten 31.
als Startpunkt.
Bei mehreren Knoten mit minimalen Grad wird aus der minimalen Knotenmenge willkürlich ein
Knoten als Startpunkt gewählt.
Für das in Abbildung 4.3 gezeigte zweidimensionale Beispiel ist dies
eindeutig Knoten 31.
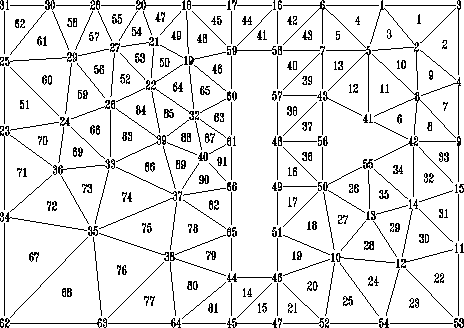
Abbildung 4.3: Mehrfachzusammenhängende Teststruktur,
66 Knoten, Knoten 41-66 sind Dirichlet-Knoten
Alle Knoten, die abhängig vom Knoten  sind, d.h. alle Einträge der Zeile
sind, d.h. alle Einträge der Zeile  , welche
aus
, welche
aus 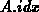 und
und 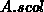 bestimmt werden, sind nach ihrem Grad aufsteigend zu sortieren.
bestimmt werden, sind nach ihrem Grad aufsteigend zu sortieren.
Beginnend mit dem kleinsten Grad sind diese Knoten in die neue 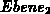 einzutragen
und fortlaufend mit zwei startend zu numerieren. Das Beispiel verlangt für den
einzutragen
und fortlaufend mit zwei startend zu numerieren. Das Beispiel verlangt für den 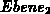 die
Knoten
die
Knoten 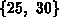 .
.
Allgemein sind für jede neue  die Abhängigkeiten jedes Knoten
die Abhängigkeiten jedes Knoten 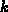 der
der  in die
in die  nach Grad sortiert einzutragen
nach Grad sortiert einzutragen ,
und eine fortlaufende Numerierung
ist zu vergeben.
Der Knoten ist aber nur dann einzutragen, wenn er noch nicht abgearbeitet wurde.
Bei Knoten gleichen Grads ist die Sortierung willkürlich vorzunehmen.
,
und eine fortlaufende Numerierung
ist zu vergeben.
Der Knoten ist aber nur dann einzutragen, wenn er noch nicht abgearbeitet wurde.
Bei Knoten gleichen Grads ist die Sortierung willkürlich vorzunehmen.
Der Algorithmus terminiert, wenn alle Knoten abgearbeitet sind.
Wurde der Startknoten aus mehren Knoten willkürlich ausgewählt, so kann es sich als günstig
erweisen, einen anderen Startknoten mit minimalen Grad auszuwählen und die Ebenenstruktur
erneut aufzubauen.
Man vergleicht alle Ebenstrukturen bzw. Neunumerierungen und wählt die Numerierung mit
dem kleinsten Profil 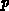 als gültige Neunumerierung aus. Um den Zeitaufwand nicht in die
Höhe zu treiben, wurde diese Möglichkeit der Optimierung jedoch nicht ausgenutzt.
als gültige Neunumerierung aus. Um den Zeitaufwand nicht in die
Höhe zu treiben, wurde diese Möglichkeit der Optimierung jedoch nicht ausgenutzt.
Die gesamte Struktur der in Abbildung 4.3 gezeigten Diskretisierung mit linearen Formfunktionen hat die folgende Abhängigkeiten:


Im wesentlichen wurde die Indexmatrix 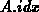 zeilenweise aufgelistet, wobei anzumerken ist, daß
hier die gesamte Matrix
zeilenweise aufgelistet, wobei anzumerken ist, daß
hier die gesamte Matrix  und nicht nur
und nicht nur  symbolisch assembliert werden muß.
symbolisch assembliert werden muß.
Die sich daraus aufbauende Ebenenstruktur

mit 12 Ebenen (E) und den 66 Knoten muß nun fortlaufend numeriert werden. Die neue
Numerierung wird in einem  -Vektor, der für eine Änderung der Knotenreferenzen
der Elemente herangezogen wird, abgespeichert.
-Vektor, der für eine Änderung der Knotenreferenzen
der Elemente herangezogen wird, abgespeichert.
Bei einer Implementierung des Cuthill-McKee-Algorithmus ist es natürlich nicht notwendig
alle Ebenen abzuspeichern. Es genügt, mit zwei Feldern der Länge  zu arbeiten,
wobei
zu arbeiten,
wobei  von
von  überschrieben wird, sobald die jeweilige
überschrieben wird, sobald die jeweilige  abgearbeitet wurde. Ein zusätzliches Feld der Länge
abgearbeitet wurde. Ein zusätzliches Feld der Länge  dient als Markerfeld, um abgearbeitete Knoten zu markieren und dort auch die neuen
Knotennummern einzutragen (
dient als Markerfeld, um abgearbeitete Knoten zu markieren und dort auch die neuen
Knotennummern einzutragen ( -Vektor).
Die Neunumerierung des Beispiels ist in Abbildung 4.4 angegeben. Der
Startknoten links oben ist in diesem Fall eindeutig.
-Vektor).
Die Neunumerierung des Beispiels ist in Abbildung 4.4 angegeben. Der
Startknoten links oben ist in diesem Fall eindeutig.
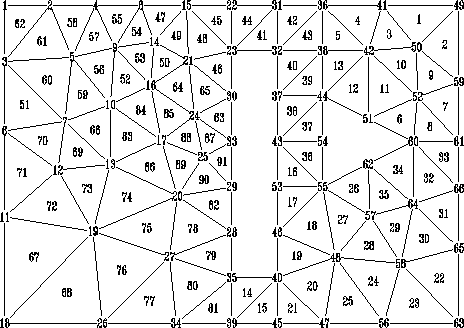
Abbildung 4.4: Mehrfachzusammenhängende Teststruktur,
Knoten nach der Cuthill-McKee-Methode geordnet
Eine einfache Modifizierung des Verfahrens, das reverse Cuthill-McKee-(RCM)-Verfahren,
ergibt vor allem bei Finite-Elemente-Gittern meist eine weitere relativ große Reduzierung
des Profils, ohne den Aufwand zu erhöhen (siehe auch Abbildung 4.5 ). Dazu
wird nach Anwendung des CM-Verfahrens im
meist eine weitere relativ große Reduzierung
des Profils, ohne den Aufwand zu erhöhen (siehe auch Abbildung 4.5 ). Dazu
wird nach Anwendung des CM-Verfahrens im  -Vektor der jeweilige Eintrag
-Vektor der jeweilige Eintrag 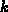 auf
auf 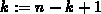 umdefiniert.
umdefiniert.
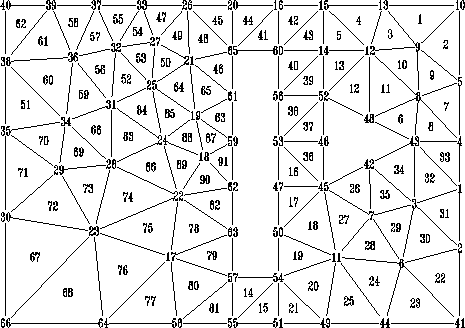
Abbildung 4.5: Mehrfachzusammenhängende Teststruktur,
Knoten nach der Reverse Cuthill-McKee-Methode geordnet
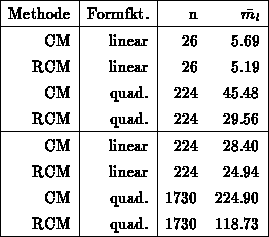
Abschließend soll noch ein quantitativer Vergleich zwischen der CM-Methode und RCM-Methode
anhand der vorgestellten Beispiele gezeigt werden.
Die Besetzungsdichte des Testbeispiels für lineare Ansatzfunktionen der strikten
unteren Dreiecksmatrix mit einem Rang von 40 hat im Mittel 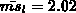 Einträge pro Zeile.
Da zur Bildung der RCM-Methode aus dem Ergebnis der CM-Methode nur die Knotennummern
über
Einträge pro Zeile.
Da zur Bildung der RCM-Methode aus dem Ergebnis der CM-Methode nur die Knotennummern
über 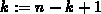 gewechselt werden, bleibt die Grundstruktur, wie auch in
den Abbildungen 4.6 und 4.7 ersichtlich ist, erhalten.
gewechselt werden, bleibt die Grundstruktur, wie auch in
den Abbildungen 4.6 und 4.7 ersichtlich ist, erhalten.
Die gemittelten Zeilenbandbreiten für die strikte untere Dreiecksmatrix 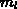 haben mit 5.17
und 5.00 für die CM und RCM Methode keine wesentlichen Verbesserungen aufzuweisen. Geht
man jedoch zu quadratischen Formfunktionen über, so erhält man ein Gleichungssystem mit
einem Rang von
haben mit 5.17
und 5.00 für die CM und RCM Methode keine wesentlichen Verbesserungen aufzuweisen. Geht
man jedoch zu quadratischen Formfunktionen über, so erhält man ein Gleichungssystem mit
einem Rang von 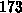 , das bei der Anwendung der CM-Methode ein
, das bei der Anwendung der CM-Methode ein 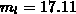 aufweist und
bei Anwendung der RCM-Methode die wesentliche Reduktion der Bandbreite auf
aufweist und
bei Anwendung der RCM-Methode die wesentliche Reduktion der Bandbreite auf 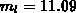 bewirkt.
bewirkt.
Die Abbildungen 4.8 und 4.9 zeigen die ungeordnete und
nach der RCM-Methode geordnete Verteilung jener Einträge der Matrix, die ungleich null sind, mit
einem Rang von 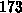 .
.
Bei dreidimensionalen Problemen ist das Verhältnis zwischen der CM- und RCM-Methode noch größer als bei zweidimensionalen Problemstellungen. Dies soll nun anhand des am Anfang des Kapitels gezeigten Beispiels (Abbildung 4.1) verifiziert werden.
Die vier unteren Zeilen setzen nicht auf der Struktur mit 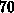 Elementen auf, sondern
die Anzahl der Tetraeder wurden über einen Verfeinerungsschritt von
Elementen auf, sondern
die Anzahl der Tetraeder wurden über einen Verfeinerungsschritt von 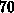 auf
auf 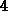 mal
mal 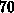 Elemente erhöht.
Da der Gaußsche Löser
Elemente erhöht.
Da der Gaußsche Löser bei einem Rang
bei einem Rang
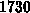 bei Verwendung einer RCM-Methode statt einer CM-Methode
um gemittelt
bei Verwendung einer RCM-Methode statt einer CM-Methode
um gemittelt 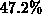 weniger Spalten pro Zeile abarbeiten muß, erzielt man hier eine
Laufzeitverbesserung des direkten Lösers um
weniger Spalten pro Zeile abarbeiten muß, erzielt man hier eine
Laufzeitverbesserung des direkten Lösers um 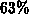 .
.



