4.3.2 Zeilenkomprimierte Struktur




Next: 4.4 Die Gauß-Transformation
Up: 4.3 Vorausberechnung der Anzahl
Previous: 4.3.1 Hüllenorientierte Struktur
Will man die Anzahl von Null verschiedenen Einträge pro Zeile der strikten unteren Dreiecksmatrix
berechnen, so ist dies wieder nur mit Hilfe einer symbolischen Vorassemblierung möglich. Jetzt ist
es jedoch im Gegensatz zu der hüllenorientierten Struktur notwendig, sich alle Spalteneinträge
einer Zeile zu merken, da sonst z.B. zwei verschiedene Elemente mit den gleichen globalen
Matrixindizes zwei Speicherplätze veranschlagen würden. Es wäre auch ineffizient, Zeile
für Zeile aufzubauen, da dies zu einer Suche nach Knotenreferenzen
in der Elementsknotenliste führt.
Die Problematik, daß man die Spaltenindizes einer Zeile speichern muß, damit getestet werden
kann, ob ein neuer Elementsindex einen zusätzlichen Eintrag bilden wird, kann nur über eine
dynamische Datenstruktur effizient gelöst werden.
Eine einfacher verkettete Liste pro Zeile zur Speicherung der Spaltenindizes ist aber auch etwas
speicherintensiver. Bei der Implementierung wurde ein Mittelweg zwischen Suchaufwand und
Speicheraufwand gewählt.
Der Vorgang, der zunächst die Elemente findet, die auf einem Knoten hängen, ist
folgender:
- Alloziere ein Knotenfeld ,,ElemOnNodeList,, der Größe der Gesamtknotenanzahl
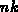 , das eine Struktur hat,
sodaß man an jedem Knoten eine einfach verkettete Liste anhängen kann und der Inhalt der
verketteten Liste Elementsnummern sind.
, das eine Struktur hat,
sodaß man an jedem Knoten eine einfach verkettete Liste anhängen kann und der Inhalt der
verketteten Liste Elementsnummern sind.
- Arbeite die Elementsliste Element für Element ab. Jeder referenzierte Knoten
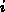 eines Elements bildet einen Eintrag in der ,,ElemOnNodeList`` bei
eines Elements bildet einen Eintrag in der ,,ElemOnNodeList`` bei 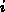 , wobei die
Elementsnummer
, wobei die
Elementsnummer 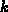 an die
zugehörige verketteten Liste angehängt wird. Sind alle Elemente abgearbeitet, so sind
Rückwärtsreferenzen vom jeweiligen Knoten zu den Elementen vollständig aufgebaut.
an die
zugehörige verketteten Liste angehängt wird. Sind alle Elemente abgearbeitet, so sind
Rückwärtsreferenzen vom jeweiligen Knoten zu den Elementen vollständig aufgebaut.
- Die Anzahl der Einträge wird nun Zeile für Zeile aufgebaut.
Dazu ist ein Zeilenfeld der Länge
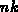 zu allozieren.
zu allozieren. Aus jeder Zeile
Aus jeder Zeile 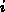 der ,,ElemOnNodeList`` werden die Elementsnummern gelesen und die
Knotenreferenzen
der ,,ElemOnNodeList`` werden die Elementsnummern gelesen und die
Knotenreferenzen 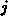 jedes Elementes im Zeilenfeld eingetragen, wobei jeder Knoten
jedes Elementes im Zeilenfeld eingetragen, wobei jeder Knoten 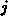 nur
dann am Ende im Zeilenfeld einzutragen ist, wenn er noch nicht im Zeilenfeld steht,
nur
dann am Ende im Zeilenfeld einzutragen ist, wenn er noch nicht im Zeilenfeld steht,
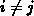 und
und 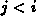 gilt. Dazu muß das Zeilenfeld vor jedem
neuen Eintrag linear abgesucht werden, da die eingetragenen Knoten nicht sortiert sind.
Da für Tetraederelemente und quadratischen Formfunktionen im Mittel etwa 10-15 Einträge
in eine Zeile
gilt. Dazu muß das Zeilenfeld vor jedem
neuen Eintrag linear abgesucht werden, da die eingetragenen Knoten nicht sortiert sind.
Da für Tetraederelemente und quadratischen Formfunktionen im Mittel etwa 10-15 Einträge
in eine Zeile 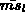 der unteren Dreiecksmatrix zu erwarten sind, ist diese Suche
nicht zeitaufwendig.
der unteren Dreiecksmatrix zu erwarten sind, ist diese Suche
nicht zeitaufwendig.Wurden alle Knoten, die zu einer Zeile gehören, gelesen, so wird
der Elementszähler in das Feld 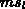 an der Stelle
an der Stelle 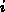 eingetragen und das Zeilenfeld bei
Bearbeitung der Zeile
eingetragen und das Zeilenfeld bei
Bearbeitung der Zeile 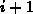 wieder überschrieben.
Nachdem die gesamte
wieder überschrieben.
Nachdem die gesamte 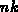 lange ,,ElemOnNodeList`` abgearbeitet wurde, sind die Einträge
der Gesamtmatrix inklusive der Dirichlet-Knoten
lange ,,ElemOnNodeList`` abgearbeitet wurde, sind die Einträge
der Gesamtmatrix inklusive der Dirichlet-Knoten 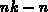 bestimmt.
bestimmt.
Zu bemerken ist, daß die Anzahl der Einträge auch für die Dirichlet-Koeffizienten
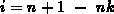 bestimmt wurde, was sinnvoll ist, da auch die Koeffizienten der rechten Seite,
die Dirichlet-Knoten
bestimmt wurde, was sinnvoll ist, da auch die Koeffizienten der rechten Seite,
die Dirichlet-Knoten 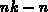 , wie schon in Abschnitt 4.3.1 erläutert,
in einer zeilenkomprimierten unteren Dreiecksmatrix gespeichert werden.
, wie schon in Abschnitt 4.3.1 erläutert,
in einer zeilenkomprimierten unteren Dreiecksmatrix gespeichert werden.




Next: 4.4 Die Gauß-Transformation
Up: 4.3 Vorausberechnung der Anzahl
Previous: 4.3.1 Hüllenorientierte Struktur
Martin Stiftinger
Fri Nov 25 16:50:24 MET 1994
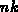 , das eine Struktur hat,
sodaß man an jedem Knoten eine einfach verkettete Liste anhängen kann und der Inhalt der
verketteten Liste Elementsnummern sind.
, das eine Struktur hat,
sodaß man an jedem Knoten eine einfach verkettete Liste anhängen kann und der Inhalt der
verketteten Liste Elementsnummern sind.
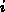 eines Elements bildet einen Eintrag in der ,,ElemOnNodeList`` bei
eines Elements bildet einen Eintrag in der ,,ElemOnNodeList`` bei 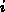 , wobei die
Elementsnummer
, wobei die
Elementsnummer 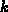 an die
zugehörige verketteten Liste angehängt wird. Sind alle Elemente abgearbeitet, so sind
Rückwärtsreferenzen vom jeweiligen Knoten zu den Elementen vollständig aufgebaut.
an die
zugehörige verketteten Liste angehängt wird. Sind alle Elemente abgearbeitet, so sind
Rückwärtsreferenzen vom jeweiligen Knoten zu den Elementen vollständig aufgebaut.
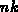 zu allozieren.
zu allozieren. Aus jeder Zeile
Aus jeder Zeile 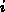 der ,,ElemOnNodeList`` werden die Elementsnummern gelesen und die
Knotenreferenzen
der ,,ElemOnNodeList`` werden die Elementsnummern gelesen und die
Knotenreferenzen 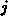 jedes Elementes im Zeilenfeld eingetragen, wobei jeder Knoten
jedes Elementes im Zeilenfeld eingetragen, wobei jeder Knoten 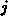 nur
dann am Ende im Zeilenfeld einzutragen ist, wenn er noch nicht im Zeilenfeld steht,
nur
dann am Ende im Zeilenfeld einzutragen ist, wenn er noch nicht im Zeilenfeld steht,
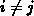 und
und 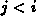 gilt. Dazu muß das Zeilenfeld vor jedem
neuen Eintrag linear abgesucht werden, da die eingetragenen Knoten nicht sortiert sind.
Da für Tetraederelemente und quadratischen Formfunktionen im Mittel etwa 10-15 Einträge
in eine Zeile
gilt. Dazu muß das Zeilenfeld vor jedem
neuen Eintrag linear abgesucht werden, da die eingetragenen Knoten nicht sortiert sind.
Da für Tetraederelemente und quadratischen Formfunktionen im Mittel etwa 10-15 Einträge
in eine Zeile 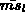 der unteren Dreiecksmatrix zu erwarten sind, ist diese Suche
nicht zeitaufwendig.
der unteren Dreiecksmatrix zu erwarten sind, ist diese Suche
nicht zeitaufwendig.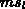 an der Stelle
an der Stelle 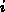 eingetragen und das Zeilenfeld bei
Bearbeitung der Zeile
eingetragen und das Zeilenfeld bei
Bearbeitung der Zeile 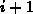 wieder überschrieben.
Nachdem die gesamte
wieder überschrieben.
Nachdem die gesamte 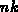 lange ,,ElemOnNodeList`` abgearbeitet wurde, sind die Einträge
der Gesamtmatrix inklusive der Dirichlet-Knoten
lange ,,ElemOnNodeList`` abgearbeitet wurde, sind die Einträge
der Gesamtmatrix inklusive der Dirichlet-Knoten 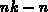 bestimmt.
bestimmt.




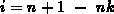 bestimmt wurde, was sinnvoll ist, da auch die Koeffizienten der rechten Seite,
die Dirichlet-Knoten
bestimmt wurde, was sinnvoll ist, da auch die Koeffizienten der rechten Seite,
die Dirichlet-Knoten