Ziel ist es, die Matrix 
in ein Produkt von Matrizen
zu überführen. Eine einmalige Zerlegung der Matrix in eine untere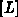 
und obere
Dreiecksmatrix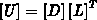 
ist hier effizienter als die Gaußsche
Elimination auf das Gesamtsystem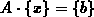 
anzuwenden, da veränderte
Randbedingungen die Koeffizientenmatrix nicht verändern. Ist nämlich eine
Dreieckszerlegung
gefunden, so kann eine effektive Lösung des Gleichungssystems in zwei Teilschritten
und
erfolgen.
Das Problem wird dadurch im wesentlichen auf eine Vorwärtselimination
und Rücksubstitution
zerlegt.
Zu erwähnen ist, daß hier eine Vorwärtselimination und Rücksubstitution für
den allgemeinen Fall gezeigt wurde. Die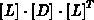 
Faktorisierung
bewirkt, daß die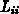 
bzw.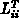 
eins sind und die Divisionen damit entfallen.
In dieser Implementierung wird die strikte untere Dreiecksmatrix zeilenweise
abgespeichert. Daher kann die Vorwärtselimination ähnlich wie in (4.13)
durchgeführt werden. Da die Rücksubstitution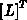 
benutzt und ein
Abarbeiten in Spalten von 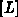ohne Suchvorgang unmöglich ist, muß auch die
Rücksubstitution zeilenweise in der Form
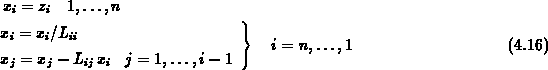
durchgeführt werden. Eine Implementierung im MCSR-Format kann aus der in Abschnitt 4.1 gezeigten Matrix-Vektor-Multiplikation gewonnen werden.
Der Vektor 
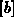kann natürlich überschrieben werden, um den zusätzlichen
Hilfsvektor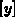 
in der Vorwärtselimination zu vermeiden.
