Die Methode der konjugierten Gradienten ist die populärste iterative Methode,
um Systeme von linearen Gleichungen zu lösen. Das Verfahren benötigt
als Ausgangspunkt eine Matrix 
, die positiv definit und symmetrisch ist.
Ist die Matrix stark besetzt, so sollte man besser auf eine Faktorisierung
der Matrix ausweichen.
Der Hauptvorteil der meisten iterativen Methoden liegt in der effizienten Nutzung
des Hauptspeichers. Die Koeffizientenmatrix bleibt während der Iteration
unverändert. Dadurch muß auch kein zusätzlicher Speicherplatz
alloziert werden.
Grundidee der Gradientenverfahren ist, die quadratische Form
zu minimieren. Diese Form besitzt unter der Voraussetzung, daß positiv definit
ist, ein Minimum. Die Werte des Lösungsvektors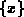 
für ein minimales 
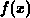kann man durch
berechnen. Die partiellen Ableitungen der quadratischen Form können in Komponentenschreibweise
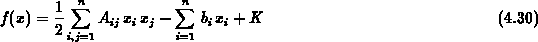
mit
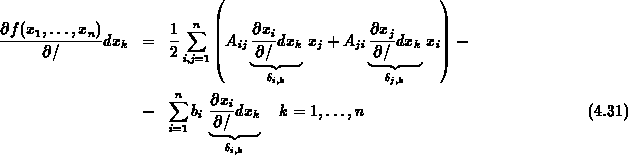
berechnet werden.
Kehrt man zu der Matrixschreibweise
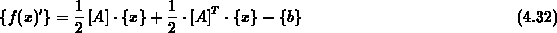
zurück und berücksichtigt die gegebene Symmetrie des Gleichungssystems, so reduziert sich die Lösung des Minimierungsproblems auf
Das Ergebnis
ist also gleich dem zu lösenden Gleichungssystem.
Vorkonditionierer