|
|
|
|
Previous: 5.3 Gradient Based Optimization Methods Up: 5.3 Gradient Based Optimization Methods Next: 5.4 Global Optimization Methods |
The Levenberg-Marquardt [96] optimizer (LMMIN) uses a so-called trust
region method where the search direction ![]() is a combination of steepest
descent and the Newton direction. The search direction is defined by:
is a combination of steepest
descent and the Newton direction. The search direction is defined by:
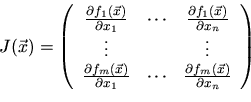
The value of ![]() is adjusted based on the last evaluation.
For a value of
is adjusted based on the last evaluation.
For a value of ![]() the direction
the direction ![]() results in the Newton
direction, whereas for
results in the Newton
direction, whereas for
![]() the direction
the direction ![]() is common to
the steepest descent method.
is common to
the steepest descent method.
The implementation used in the presented examples is based on the MINPACK project [97,98].
2003-03-27