previous up next Dissertation Thomas Binder contents
 Previous: Job Farming Facility   Up: 5. Optimization for TCAD   Next: Levenberg-Marquardt Optimizer

5.3 Gradient Based Optimization Methods

Gradient based optimization strategies iteratively search a minimum of a $ D$ dimensional target function $ f(\vec{x})$. The target function is thereby approximated by a terminated Taylor series expansion around $ \vec{x_0}$:

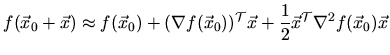
$\displaystyle f(\vec{x}_0 + \vec{x}) \approx f(\vec{x}_0) + (\nabla f(\vec{x}_0... ...mathcal{T}\vec{x} + \frac{1}{2}\vec{x}^\mathcal{T}\nabla^2 f(\vec{x}_0)\vec{x} $

The actual optimization is performed iteratively. After an initial value $ \vec{x}_{i=0}$ was chosen and the target function $ f(\vec{x}_i)$ was computed, the following loop tries to achieve a minimum:

  1. Check the convergence criterion of $ f(\vec{x}_i)$; terminate with $ \vec{x}_i$ as the solution if fulfilled.
  2. Compute a direction $ \vec{p}_i$ and a step width $ l_i$
  3. Evaluate the new point $ \vec{x}_{i+1}=\vec{x}_i+\vec{p}_i\cdot l_i$; compute the target $ f(\vec{x}_{i+1})$ and go to step 1.

To compute the step direction $ p_i$ a linear approximation (first order) of the target function can be used:

$\displaystyle f(\vec{x}_0+\vec{p})\approx f(\vec{x}_0)+(\nabla f(\vec{x}_0))^\mathcal{T}\vec{p}$

which results in the step direction:

$\displaystyle \vec{p}=-\nabla f(\vec{x}_0)$

This is called the steepest descent method. A second order approach uses a quadratic approximation:

$\displaystyle \nabla f(\vec{x}_0) + \nabla^2 f(\vec{x}_0)\,\vec{p} = 0$

This is referred to as Newton's direction method.

To compute the step width $ l_k$ the parameter vector of the next iteration is calculated by

$\displaystyle \vec{x}_{k+1}=\vec{x}_k+\alpha_k\vec{p}_k$

The parameter $ \alpha_k$ denotes the step width and is chosen depending on the used optimization algorithm.

For an analytically given target function the first and second order derivatives can directly be transferred into a computer program, however if no explicit formula can be defined, the target is computed numerically by means of a simulation. In this case approximations for the derivatives are necessary. In the following the approximation of a univariate target function $ f(x)$ is given. For multivariate target functions the finite difference approximation is applied for each dimension.

The performance of a gradient based method strongly depends on the initial values supplied. Several optimization runs with different initial values might be necessary if no a priori knowledge (e.g., the result of a process simulation) about the function to optimize can be applied.


Subsections


previous up next   contents
 Previous: Job Farming Facility   Up: 5. Optimization for TCAD   Next: Levenberg-Marquardt Optimizer
2003-03-27