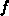 definierte Größe
definierte Größe 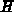 niemals zunehmen kann,
sondern immer abnehmen oder konstant bleiben muß, wenn
niemals zunehmen kann,
sondern immer abnehmen oder konstant bleiben muß, wenn 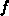 der
Boltzmanngleichung genügt [34]:
der
Boltzmanngleichung genügt [34]:




Boltzmann hat gezeigt, daß in einem idealen Gas eine beliebige
Anfangsverteilung der Moleküllagen und -geschwindigkeiten in einen
Gleichgewichtszustand übergeht, in dem die Molekülgeschwindigkeiten
dem Maxwellschen Gesetz gemäß verteilt sind.
Der Beweis beruht darauf zu zeigen, daß eine mittels der
Verteilungsfunktion 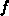 definierte Größe
definierte Größe 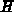 niemals zunehmen kann,
sondern immer abnehmen oder konstant bleiben muß, wenn
niemals zunehmen kann,
sondern immer abnehmen oder konstant bleiben muß, wenn 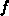 der
Boltzmanngleichung genügt [34]:
der
Boltzmanngleichung genügt [34]:
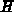 hat die Eigenschaft unter der Wirkung
von Zusammenstößen solange abzunehmen, bis sich die
Boltzmann-Maxwellsche Gleichgewichtsverteilung
hat die Eigenschaft unter der Wirkung
von Zusammenstößen solange abzunehmen, bis sich die
Boltzmann-Maxwellsche Gleichgewichtsverteilung 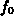 einstellt.
Weil die Hilfsfunktion
einstellt.
Weil die Hilfsfunktion 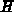 mit der Entropie in enger Beziehung steht, ist
dieses Ergebnis dem Beweis äquivalent, daß die Entropie
eines abgeschlossenen Systems nicht abnehmen kann.
Auf diese Weise liefert das H-Theorem eine mikroskopische Deutung des zweiten
Hauptsatzes der Thermodynamik.
mit der Entropie in enger Beziehung steht, ist
dieses Ergebnis dem Beweis äquivalent, daß die Entropie
eines abgeschlossenen Systems nicht abnehmen kann.
Auf diese Weise liefert das H-Theorem eine mikroskopische Deutung des zweiten
Hauptsatzes der Thermodynamik.
Um das H-Theorem auf den thermoelektrischen Transport im Halbleiter anwenden
zu können, muß eine Bilanzgleichung der Form (2.165) für ein mit
Hilfe von Gl. (2.157) definiertes lokales 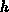 ermittelt werden.
Die zu (4.43) äquivalente lokale Formulierung des H-Theorem
für kontinuierliche thermodynamische Systeme lautet:
ermittelt werden.
Die zu (4.43) äquivalente lokale Formulierung des H-Theorem
für kontinuierliche thermodynamische Systeme lautet:
Die Anwendung des H-Theorems auf Kristallelektronen verlangt die Verwendung der Fermi-Diracstatistik. Die Vernachlässigung des Verlustes von Elektronen durch Rekombinationsprozesse bedeutet eine Beschränkung auf die Erfassung der primär interessierenden vektoriellen Beiträge zur Entropieproduktion. Indem gezeigt wird, wie Stoßprozesse zu einem Anwachsen der Entropie führen, kann die Irreversibilität der im Halbleiter stattfindenden Transportprozesse erklärt werden. Dadurch ist es möglich, die Energieumwandlung, wie sie sich auf makroskopischer Ebene zeigt, mit im Halbleiter stattfindenden, mikroskopischen Prozessen in Beziehung zu setzen.
In der kinetischen Theorie ist 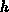 definiert als [86], [180],
[199]:
definiert als [86], [180],
[199]:
 ist eine Hilfsgröße, die für Boltzmannteilchen den Wert
ist eine Hilfsgröße, die für Boltzmannteilchen den Wert 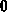 , für
Fermi-Diracteilchen
, für
Fermi-Diracteilchen 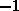 und für Bose-Einsteinteilchen
und für Bose-Einsteinteilchen 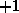 annimmt.
Leitet man Gl. (4.45) nach der Zeit ab, ergibt sich:
annimmt.
Leitet man Gl. (4.45) nach der Zeit ab, ergibt sich:
Die Zeitableitung der Verteilungsfunktion kann mit Hilfe der Boltzmanngleichung (2.74) ausgedrückt werden:
Das Integral des 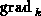 -Terms
kann in ein Oberflächenintegral über die unendlich ferne Kugel
im
-Terms
kann in ein Oberflächenintegral über die unendlich ferne Kugel
im 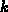 -Raum umgewandelt werden.
Da dort - wegen der Endlichkeit der Energie -
-Raum umgewandelt werden.
Da dort - wegen der Endlichkeit der Energie - 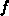 verschwindet, ist das Integral null.
Formt man die verbleibenden Ausdrücke in Gl. (4.47) um, erhält man
die gesuchte Bilanzgleichung für
verschwindet, ist das Integral null.
Formt man die verbleibenden Ausdrücke in Gl. (4.47) um, erhält man
die gesuchte Bilanzgleichung für 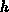 :
:
Das Integral der linken Seite entspricht der Divergenz von 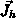 .
Die rechte Seite von Gl. (4.48) stellt den Quellterm
.
Die rechte Seite von Gl. (4.48) stellt den Quellterm 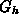 dar.
dar.
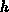 ist auf einfache Weise mit der Entropiedichte verknüpft [199]:
ist auf einfache Weise mit der Entropiedichte verknüpft [199]:
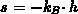 .
Linearisiert man Gl. (4.48) und multipliziert mit
.
Linearisiert man Gl. (4.48) und multipliziert mit 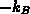 , erhält
man die Entropiebilanzgleichung der kinetischen Theorie.
Die Entropiequellstärke
, erhält
man die Entropiebilanzgleichung der kinetischen Theorie.
Die Entropiequellstärke 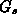 folgt unmittelbar aus:
folgt unmittelbar aus:
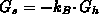 .
.
Der Stoßterm in Gl. (4.48) kann mit Hilfe des
Strömungsvektors 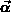 ausgedrückt werden.
Gl. (2.82) läßt sich unter Berücksichtigung von
Gl. (2.76) folgendermaßen umformen:
ausgedrückt werden.
Gl. (2.82) läßt sich unter Berücksichtigung von
Gl. (2.76) folgendermaßen umformen:
Für Fermi-Diracteilchen (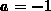 ) vereinfacht sich der Klammerausdruck
der rechten Seite der Bilanzgleichung (4.48).
Entwickelt man ihn um die Gleichgewichtsverteilungsfunktion
) vereinfacht sich der Klammerausdruck
der rechten Seite der Bilanzgleichung (4.48).
Entwickelt man ihn um die Gleichgewichtsverteilungsfunktion 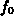 erhält
man [199]:
erhält
man [199]:
Nur der letzte Term liefert einen Beitrag zur Entropieproduktion.
Faßt man die Ergebnisse zusammen, läßt sich mit Hilfe
von Gl. (4.49) und (4.50) die Entropiequelle 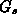 ermitteln:
ermitteln:
Weil der Strömungsvektor 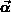 nach Gl. (2.82)
den treibenden Kräften proportional ist, erlauben
Gl. (2.83), (2.84), (2.85), (2.86), (2.87)
unmittelbar, die Entropieproduktion (4.51) in die Form
konjugierter thermodynamischer Flüsse und Kräfte zu bringen:
nach Gl. (2.82)
den treibenden Kräften proportional ist, erlauben
Gl. (2.83), (2.84), (2.85), (2.86), (2.87)
unmittelbar, die Entropieproduktion (4.51) in die Form
konjugierter thermodynamischer Flüsse und Kräfte zu bringen:
Der besondere Vorteil dieser Formulierung ist die Möglichkeit, Zusammenhänge zwischen (makroskopischen) Energien und Energiestromdichten des Elektronensystems mit (mikroskopischen) Energien des einzelnen Elektrons herzustellen. Somit kann die physikalische Bedeutung von Größen der irreversiblen Thermodynamik mit den Mitteln der kinetischen Theorie transparent gemacht werden.
Gl. (4.57), (4.58), (4.59), (4.60) enthalten
Flußgrößen, die den treibenden Kräften konjugiert sind.
Gl. (4.57) ist sowohl Gl. (4.52) als auch (4.53)
zuzuordnen.
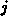 bezeichnet den Teilchenstrom der Elektronen nach Gl. (2.37).
Der Gesamtenergiefluß (Fluß der totalen inneren Energie) des
Elektronensystems
bezeichnet den Teilchenstrom der Elektronen nach Gl. (2.37).
Der Gesamtenergiefluß (Fluß der totalen inneren Energie) des
Elektronensystems 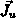 ist durch die Definitionsgleichung
(2.39) mit der Gesamtenergie
ist durch die Definitionsgleichung
(2.39) mit der Gesamtenergie 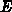 des einzelnen Elektrons verknüpft.
Der Fluß der inneren Energie (im eigentlichen Sinn) des Elektronensystems
kann mit Hilfe der kinetischen Energie
des einzelnen Elektrons verknüpft.
Der Fluß der inneren Energie (im eigentlichen Sinn) des Elektronensystems
kann mit Hilfe der kinetischen Energie  des einzelnen Elektrons
definiert werden:
des einzelnen Elektrons
definiert werden:
Die Entropiestromdichte ist:
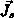 folgt auch aus Gl. (4.48), wenn der Integrand der
linken Seite um
folgt auch aus Gl. (4.48), wenn der Integrand der
linken Seite um 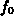 entwickelt wird (mit
entwickelt wird (mit 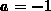 ) [199].
Vergleicht man die Definition der Entropiestromdichte (4.62) mit der
Definition der Gesamtstromdichte (2.39) bzw. dem Fluß der inneren
Energie (4.61), ergeben sich folgende Zusammenhänge:
) [199].
Vergleicht man die Definition der Entropiestromdichte (4.62) mit der
Definition der Gesamtstromdichte (2.39) bzw. dem Fluß der inneren
Energie (4.61), ergeben sich folgende Zusammenhänge:
Gl. (4.63) bestätigt die makroskopische Definition der
Wärmeflüsse (4.28), (4.29) und (3.37).
In der formalen Transporttheorie wird der Wärmestrom
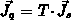 in Übereinstimmung mit Gl. (4.63)
in Anlehnung an die Gibbs Fundamentalform
in Übereinstimmung mit Gl. (4.63)
in Anlehnung an die Gibbs Fundamentalform 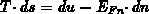 bzw.
bzw.
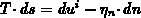 eingeführt
[120], [121], [153], [197].
Die (makroskopische) Gesamtenergie
eingeführt
[120], [121], [153], [197].
Die (makroskopische) Gesamtenergie  (totale innere Energie) des
Elektronensystems entspricht der (mikroskopischen) Gesamtenergie
(totale innere Energie) des
Elektronensystems entspricht der (mikroskopischen) Gesamtenergie 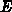 des
einzelnen Elektrons im Banddiagramm.
Die (makroskopische) innere Energie (im engen Sinn)
des
einzelnen Elektrons im Banddiagramm.
Die (makroskopische) innere Energie (im engen Sinn) 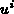 kann der
(mikroskopischen) kinetischen Energie
kann der
(mikroskopischen) kinetischen Energie  zugeordnet werden.
zugeordnet werden.



