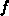 als Summe
der Gleichgewichtsverteilung
als Summe
der Gleichgewichtsverteilung 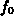 und einer durch äußere
Kräfte verursachten Störung
und einer durch äußere
Kräfte verursachten Störung 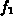 dargestellt werden kann:
dargestellt werden kann:




Zwei Näherungen, die Relaxationszeitnäherung und die Linearisierung, ermöglichen eine analytische Lösung der Boltzmanngleichung.
Mit Hilfe der Relaxationszeitnäherung kann der Stoßterm in
Gl. (2.74) entscheidend vereinfacht werden.
Es wird angenommen, daß die Nichtgleichgewichtsverteilung 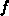 als Summe
der Gleichgewichtsverteilung
als Summe
der Gleichgewichtsverteilung 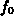 und einer durch äußere
Kräfte verursachten Störung
und einer durch äußere
Kräfte verursachten Störung 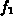 dargestellt werden kann:
dargestellt werden kann:
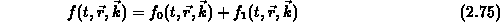
Gemäß der Vorstellung, daß die Rückkehr in den
Gleichgewichtszustand aufgrund von Stoßprozessen exponentiell mit
der Relaxationszeit  erfolgt, ergibt sich folgender Ansatz:
erfolgt, ergibt sich folgender Ansatz:
Die Relaxationszeit ist im allgemeinen von Zeit, Ort und Kristallimpuls abhängig. Die Anwendbarkeit der Relaxationszeitnäherung ist von der Bedingung isotroper oder elastischer Streuprozesse abhängig [120]. Bei elastischer Streuung ändern die Ladungsträger durch Stöße lediglich die Bewegungsrichtung, verlieren aber keine Energie. Bei isotroper Streuung besteht zwischen den Richtungen vor und nach dem Stoß keine Beziehung (erinnerungslöschender Stoß). Gewöhnlich wird die Relaxationszeit als Funktion der kinetischen Energie dargestellt [121], [192]:
Der numerische Parameter  nimmt für verschiedene Streumechanismen
verschiedene Werte an.
nimmt für verschiedene Streumechanismen
verschiedene Werte an.
Während die rechte Seite von (2.74) wegen der
Relaxationszeitnäherung (2.76) nur 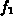 enthält,
erlaubt die Linearisierung der Boltzmanngleichung
die Nichtgleichgewichtsverteilung
enthält,
erlaubt die Linearisierung der Boltzmanngleichung
die Nichtgleichgewichtsverteilung 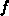 der linken Seite von (2.74)
durch die Gleichgewichtsverteilung
der linken Seite von (2.74)
durch die Gleichgewichtsverteilung 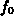 zu ersetzen.
Diese Vereinfachung ist gleichbedeutend mit
der Annahme, daß die Gradienten der Gleichgewichtsverteilung
(im Orts- und Impulsraum) sehr viel größer sind als die der Störung
zu ersetzen.
Diese Vereinfachung ist gleichbedeutend mit
der Annahme, daß die Gradienten der Gleichgewichtsverteilung
(im Orts- und Impulsraum) sehr viel größer sind als die der Störung
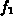 .
Die Linearisierung der Boltzmanngleichung impliziert auch, daß die
äußere Kraft
.
Die Linearisierung der Boltzmanngleichung impliziert auch, daß die
äußere Kraft 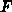 als Gradient eines Skalarpotentials dargestellt
werden kann.
Sollen Magnetfelder berücksichtigt werden,
muß
als Gradient eines Skalarpotentials dargestellt
werden kann.
Sollen Magnetfelder berücksichtigt werden,
muß 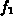 auch im Feldterm der Boltzmanngleichung berücksichtigt
werden [121], [153].
auch im Feldterm der Boltzmanngleichung berücksichtigt
werden [121], [153].
Setzt man Gl. (2.76) als Approximation des Stoßterms in die Boltzmanngleichung (2.74) ein, läßt sich - unter der Voraussetzung der Nichtberücksichtigung magnetischer Felder - die Lösung der Boltzmanngleichung in erster Näherung (Linearisierung) unmittelbar anschreiben:
Die Änderung der Gleichgewichtsverteilungsfunktion 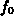 mit dem
Wellenvektor ergibt sich aufgrund der k-Abhängigkeit der Bandstruktur:
mit dem
Wellenvektor ergibt sich aufgrund der k-Abhängigkeit der Bandstruktur:
Setzt man Gl. (2.79) in Gl. (2.78) ein, erhält man:
Der Klammerausdruck in Gl. (2.80) wird auch als Strömungsvektor bezeichnet [52], [198]. Seine explizite Form ergibt sich, wenn der Gradient der Gleichgewichtsverteilungsfunktion berechnet wird:
Die endgültige Form der Relaxationszeitlösung der Boltzmanngleichung erhält man, indem man Gl. (2.80), (2.81), (2.35) zusammenfaßt:
Der Strömungsvektor 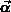 ist einer allgemeinen treibenden Kraft
ist einer allgemeinen treibenden Kraft
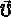 proportional.
proportional.
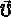 kann als Resultierende einzelner treibender Kräfte, z.B.
der Gradienten des elektrostatischen Potentials,
der Ladungsträgerkonzentrationen und
der Temperatur, begriffen werden.
kann als Resultierende einzelner treibender Kräfte, z.B.
der Gradienten des elektrostatischen Potentials,
der Ladungsträgerkonzentrationen und
der Temperatur, begriffen werden.
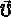 hat verschiedene äquivalente Formen:
hat verschiedene äquivalente Formen:
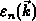 ist allein vom Wellenvektor
ist allein vom Wellenvektor 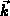 abhängig.
Die Gesamtenergie
abhängig.
Die Gesamtenergie 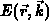 ist sowohl vom Ort wie vom Wellenvektor
abhängig.
Quasifermienergie
ist sowohl vom Ort wie vom Wellenvektor
abhängig.
Quasifermienergie 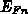 und Temperatur
und Temperatur 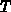 sind nur ortsabhängig.
Die resultierende treibende Kraft setzt sich aus verschiedenen einzelnen
treibenden Kräften zusammen.
Die Transformation der einzelnen treibenden Kräfte ist mit einer
Transformation der Transportkoeffizienten verbunden.
Gl. (2.83) folgt direkt aus Gl. (2.81).
Verwendet man Gl. (2.47) statt Gl. (2.48) ergibt sich
Gl.(2.84).
Gl. (2.84) folgt aufgrund der Definition der Gesamtenergie des
Elektrons (2.22)
und der Quasifermienergie (2.45) auch unmittelbar aus Gl. (2.83).
Gl. (2.85), (2.86), (2.87) ergeben sich durch Anwendung
der Produktregel unter Berücksichtigung von
Gl. (2.22), (2.24) und (2.45).
sind nur ortsabhängig.
Die resultierende treibende Kraft setzt sich aus verschiedenen einzelnen
treibenden Kräften zusammen.
Die Transformation der einzelnen treibenden Kräfte ist mit einer
Transformation der Transportkoeffizienten verbunden.
Gl. (2.83) folgt direkt aus Gl. (2.81).
Verwendet man Gl. (2.47) statt Gl. (2.48) ergibt sich
Gl.(2.84).
Gl. (2.84) folgt aufgrund der Definition der Gesamtenergie des
Elektrons (2.22)
und der Quasifermienergie (2.45) auch unmittelbar aus Gl. (2.83).
Gl. (2.85), (2.86), (2.87) ergeben sich durch Anwendung
der Produktregel unter Berücksichtigung von
Gl. (2.22), (2.24) und (2.45).



