 durch
durch 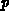 ersetzt wird und die beiden letzten
Beiträge zur Wärmegeneration negativ genommen werden, ergibt sich
die hydrodynamische Energiebilanzgleichung
der Löcher:
ersetzt wird und die beiden letzten
Beiträge zur Wärmegeneration negativ genommen werden, ergibt sich
die hydrodynamische Energiebilanzgleichung
der Löcher:




Die hydrodynamische Behandlung des thermoelektrischen Transports basiert auf der Momentenentwicklung der Boltzmanngleichung (2.74). Ausgangspunkt ist die hydrodynamische Energiebilanzgleichung der Elektronen (2.128), die das zweite Moment der Boltzmanngleichung darstellt [155].
Wenn in Gl. (2.128)  durch
durch 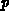 ersetzt wird und die beiden letzten
Beiträge zur Wärmegeneration negativ genommen werden, ergibt sich
die hydrodynamische Energiebilanzgleichung
der Löcher:
ersetzt wird und die beiden letzten
Beiträge zur Wärmegeneration negativ genommen werden, ergibt sich
die hydrodynamische Energiebilanzgleichung
der Löcher:
Gl. (4.64) berücksichtigt die Definition der Nettorekombinationrate
(2.122).
Für das Phononensystem gilt Gl. (4.42).
Aus Gründen einer einheitlichen Bezeichnungsweise wird
ein Streuterm 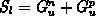 eingeführt.
eingeführt.
Vernachlässigt man den Beitrag der Driftenergie zur Energiedichte 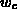 , gilt
nach Gl. (2.116) die Näherung:
, gilt
nach Gl. (2.116) die Näherung:
In Gl. (4.65) wird das Elektronen- bzw. Löcherkollektiv als ideales
Gas betrachtet.
Die Energiedichte des Gitters läßt sich mit Hilfe der
Wärmekapazität 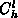 und der Gittertemperatur
und der Gittertemperatur 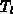 ausdrücken:
ausdrücken:
Setzt man eine einheitliche Temperatur 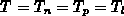 voraus, können
die Energiebilanzgleichungen des Elektronen-, Löcher- und Phononensystems
zu einer Wärmeflußgleichung des Halbleiters zusammengefaßt
werden [155]:
voraus, können
die Energiebilanzgleichungen des Elektronen-, Löcher- und Phononensystems
zu einer Wärmeflußgleichung des Halbleiters zusammengefaßt
werden [155]:
Dabei muß berücksichtigt werden, daß die Streuterme folgender Beziehung genügen [146], [152], [155]:
Die gesamte Wärmeleitfähigkeit des Halbleiters setzt sich aus den
einzelnen Beiträgen der Teilsysteme zusammen
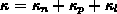 .
Die gesamte Wärmekapazität ist:
.
Die gesamte Wärmekapazität ist: