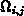6.2.1 Ortsdiskretisierung

Die Ortsdiskretisierung erfolgt mit Hilfe 'Finiter Boxen'. Sie basieren auf der Idee sogenannter 'Terminating Lines' [6] und stellen eine Verallgemeinerung Finiter Differenzen dar [72], [69], [168].

Die Diskretisierung der Gleichungen mittels Finiter Differenzen kann auf drei verschiedene Arten durchgeführt werden: Ersetzen der Differentiale durch Differenzen, mit Hilfe einer Taylorreihenentwicklung oder durch Anwendung der Boxintegrationsmethode (Finite Volumsmethode, Kontrollvolumensmethode) [23], [61], [125], [168], [178]. Die Boxintegrationsmethode stellt eine flußkonservierende Diskretisierungsmethode dar. Sie liefert eine unmittelbar diskrete Formulierung von Erhaltungsprinzipien in koordinatensystembezogenen Kontrollvolumina, aus denen das Simulationsgebiet zusammengesetzt ist. Die Boxintegrationsmethode ist nicht auf rechtwinkelige Kontrollvolumina beschränkt und eignet sich deshalb auch zur Diskretisierung nichtplanarer Strukturen.

Der Ausgangspunkt der Boxintegrationsmethode ist die Anwendung der integralen Form der stationären Kontinuitätsgleichung (2.163) bzw. (2.164) auf eine Elementarzelle (Kontrollvolumen) 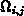[168]:

Die Elementarzelle 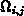wird von der Oberfläche 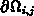begrenzt. Das Simulationsgebiet besteht aus einer Vielzahl von Elementarzellen. Jede einzelne stellt ein Kontrollvolumen dar, für das eine oder mehrere Kontinuitätsgleichungen gelten. Jedem einzelnen Kontollvolumen wird ein Gitterpunkt zugeordnet. In Gl. (6.1) bedeutet 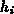den Abstand von einem Gitterpunkt mit den Indizes 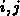zum nächsten in Richtung der positiven -Achse. 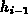ist der Abstand zum Nachbarpunkt in negativer -Richtung. Analoges gilt für 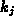, 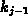(positive bzw. negative y-Richtung). Die Elementarzelle reicht nach Gl. (6.1) in jeder Koordinatenrichtung jeweils bis zur Mitte des Abstandes zum jeweiligen Nachbarpunkt.

Für rechtwinkelige, zweidimensionale Elementarzellen in einem kartesischen Koordinatensystem herrschen besonders einfache Verhältnisse:

Die Durchführung der Diskretisierung erfolgt in zwei Schritten. Zunächst wird ausgehend von Gl. (6.2) der Divergenzoperator der Kontinuitätsgleichung diskretisiert. Anschließend erfolgt die Diskretisierung der Flüsse, indem sie auf die abhängigen Variablen an den Gitterpunkten zurückgeführt werden. Der vordere bzw. hintere Differenzenquotient wird verwendet, um die Flußgrößen an den Halbpunkten in jeweils negativer und positiver Richtung zu bestimmen. Insgesamt ergibt sich der mittlere Differenzenqotient, der den Mittelwert des vorderen und hinteren Differenzenquotienten darstellt.

Die Diskretisierung des Divergenzoperators der Wärmeflußgleichung erfolgt analog zur Poisson- bzw. Kontinuitätsgleichung [65], [69], [168]:

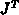bezeichnet den Anteil des Wärmestromes durch Wärmeleitung (ohne Wärmekonvektion). Die Indizierung der diskreten Flußgrößen folgt folgender Konvention: 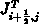bedeutet den Wert der Stromdichte am Ort 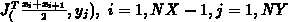. 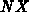, 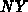bezeichnen die Anzahl der Gitterlinien in - und 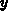-Richtung. Flußgrößen werden zwischen zwei benachbarten Gitterpunkten als konstant angenommen.

Im nächsten Schritt werden die Flüsse an den Halbpunkten auf die korrespondierende abhängige Variable in den Gitterpunkten zurückgeführt. Im Fall der Wärmeflußgleichung erhält man für den Halbpunkt in positiver x-Richtung (+x):

Setzt man Gl. (6.4) und analoge Ausdrücke für die restlichen drei Koordinatenrichtungen (+y,-x,-y) in Gl. (6.3) ein, ergibt sich für einen regulären, inneren Punkt mit 4 Nachbarn eine 5-Punkt-Formel :

Die diskreten Temperaturwerte werden in Gl. (6.5) gegen den Uhrzeigersinn durchlaufen.

In einem Gitter, das aus Finiten Boxen besteht, können Gitterlinien innerhalb des Simulationsgebietes enden. In diesem Fall fehlt am Endpunkt einer Gitterlinie ein Nachbarpunkt (sogenannte 'Terminating Line'). Um eine Differenzengleichung von derselben Ordnung wie für einen regulären, inneren Punkt zu erhalten, müssen die ersten Ableitungen der abhängigen Variablen, d.h. die korrespondierenden Flußgrößen zur linearen Interpolation benutzt werden [72], [168]. Dadurch ergibt sich für die Differenzenapproximation des Laplaceoperators ein 6-Punkt- anstatt eines 5-Punkt-Schemas.

Fehlt der Nachbar, z.B. in positiver x-Richtung, muß Gl. (6.4) durch folgenden Ausdruck ersetzt werden:

Setzt man Gl. (6.6) in Gl. (6.3) ein, erhält man eine 6-Punkt-Formel für einen irregulären inneren Punkt (mit 'Terminating Line' in positiver x-Achse):

Mit der Diskretisierung der Stromrelationen (3.89), (3.90), d.h. der Bestimmung der elektrischen Stromdichten in den Halbpunkten, sind spezifische Schwierigkeiten verbunden. Weil sich die Ladungsträgerkonzentrationen gewöhnlich exponentiell mit dem elektrostatischen Potential zwischen benachbarten Gitterpunkten ändern, ist die Diskretisierung der Stromrelationen etwas komplizierter. Eine analoge Diskretisierung wie für den Wärmefluß (6.4) stellt sich als numerisch instabil heraus [50], [162], [178], [167], [168].

Die für diese Instabilität entscheidende formale Besonderheit der Stromrelation ist die Tatsache, daß die Lösungsvariable 'Ladungsträgerkonzentration' in ihr doppelt aufscheint. Sie kommt einmal direkt vor und tritt noch einmal in Verbindung mit dem Gradienten auf. Es wird angenommen, daß sich die Beweglichkeit zwischen Gitterpunkten nur langsam ändert, sodaß sie im Gitterintervall als konstant betrachtet werden kann (keine Diskretisierung der Beweglichkeit).

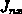sei

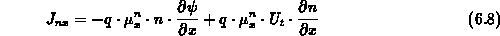
die x-Komponente der Elektronenstromdichte in der Drift-Diffusionsnäherung (2.131). Unter der Annahme, daß sich nicht nur das Potential sondern auch die Ladungsträgerdichten zwischen zwei Gitterpunkten linear ändern, kann die Stromdichte im Halbpunkt folgendermaßen approximiert werden:

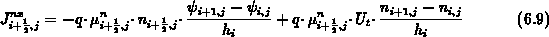
Im Gleichgewicht kompensiert sich der Drift- und Diffusionsanteil. Der Gesamtstrom muß null sein:

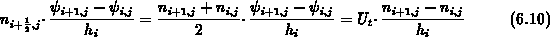
Daraus ergibt sich durch Umformung:

Unter der Annahme, daß 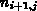durch die Dotierung bestimmt ist, stellt Gl. (6.11) eine Bestimmungsgleichung für 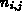als Funktion der Potentialdifferenz zwischen zwei Nachbarpunkten dar. Gl. (6.11) liefert unphysikalische, negative Konzentrationswerte 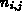, wenn die Potentialdifferenz zwischen benachbarten Punkten größer als die doppelte Thermospannung 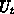beträgt.

Um diese Schwierigkeiten zu vermeiden, wird die Diskretisierung der Stromrelationen üblicherweise nach der Methode von Scharfetter-Gummel [163], [168] durchgeführt. Die Idee ist, die gesuchten Größen 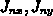in Intervallmitte zu berechnen, indem eine gewöhnliche Differentialgleichung im Intervall 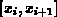mit geeigneten Randbedingungen (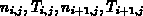) gelöst wird. Allerdings ist die Scharfetter-Gummel-Diskretisierung ursprünglich nur auf die einfache Drift-Diffusionsgleichung (2.131) bei konstanter Temperatur angewandt worden. Sie kann aber für den thermoelektrischen Transport verallgemeinert werden, um inhomogene Temperaturen zu berücksichtigen.

Ausgangsspunkt ist die eindimensionale Formulierung der Stromrelationen in der Form (3.89), (3.90). Aus notationstechnischen Gründen wird ein effektives Potential 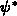definiert:

Der Einfachheit wegen wird in den folgenden Formeln 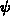statt 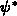geschrieben. Die x-Komponente der skalierten Elektronenstromdichte kann in folgende Form gebracht werden:

ist ein Gewichtsfaktor, der von der effektiven thermoelektrischen Kraft (Soretfaktor) abhängt. Gl. (6.13) stellt eine lineare Differentialgleichung erster Ordnung dar, deren Koeffizienten im Unterschied zum klassischen Scharfetter-Gummel-Verfahren keine Konstanten, sondern stetige Funktionen der -Koordinate sind. Der Grund dafür ist darin zu sehen, daß im nichtisothermischen Fall zusätzlich zu den in (3.89), (3.90) getroffenen Voraussetzungen der Konstanz der Beweglichkeit und der linearen Abhängigkeit des elektrostatischen Potentials von der -Koordinate, angenommen wird, daß auch die Temperatur eine lineare Funktion der Ortskoordinate zwischen zwei Gitterpunkten ist. Gl. (6.13) kann mit elementaren Methoden (Separation der Variablen und Variation der Konstanten nach Lagrange [25], [31]) gelöst werden:

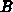bezeichnet die Bernoulli Funktion, die folgendermaßen definiert ist [163], [168]:

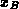ist das Argument der Bernoulli Funktion:

Ähnliche Ausdrücke ergeben sich für die restlichen drei Koordinatenrichtungen. Die Berechnung der Löcherstromdichten in den Halbpunkten erfolgt auf analoge Weise.

Faßt man die diskretisierte Elektronenkontinuitätsgleichung und die gewonnenen Ausdrücke der Elektronenstromdichten an den Halbpunkten zusammen, erhält man für einen regulären Gitterpunkt im Inneren des Rechengebietes:

Der analoge Ausdruck für Löcher lautet:

Es läßt sich zeigen, daß im isothermen Grenzfall (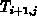= 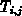usw.) aus Gl. (6.14), (6.16) bzw. Gl. (6.18), (6.17) die klassische Form der diskretisierten Stromrelationen für konstante Temperatur folgt [128], [195].

Die Diskretisierung der Randbedingungen erfolgt wie in [68], [69], [70], [104], [105], [141] Die Berücksichtigung gemischter Randbedingungen in der Wärmeflußgleichung ergibt eine modifizierte Struktur der Jakobimatrix.

Die beschriebene Erweiterung der Scharfetter-Gummel-Diskretisierung impliziert die Konstanz der Beweglichkeit zwischen Gitterpunkten. Diese Forderung ist im thermoelektrischen Fall gut erfüllt, weil nur moderate Temperaturgradienten auftreten.