Fick's diffusion laws
The laws of diffusion are mathematical relationships which relate the rate of diffusion to the concentration gradient for net mass transfer. Such laws are considered to be phenomenological. We define vector
Diffusion is the kinetic process that leads to the homogenization, or uniform mixing, of the chemical components in a phase. Although mixing in a fluid (liquid or gas) may occur on many length scales, as induced by macroscopic flow, diffusive mixing in solids, by contrast, occurs only on the atomic or molecular level. As time increases, the extent of homogenization by diffusion also increases, and the length scale over which chemical homogeneity persists within a phase gradually extends to macroscopic distances.
In the silicon process technology, depending on the complexity of the model, dopant redistribution does not only include dopant atoms itself, but also point defects. The point defects can be divided into simple and extended point defects.
Additionally, the presence of the large number of the charged dopant atoms causes an electrical field in the inside of the wafer, which reversely influences the diffusion of dopants.
The continuum-based diffusion models are successfully applied in many process simulation programs [6]. These models use the so-called methodology of diffusion-reaction equations, which was shown to be very efficient for the numerical simulation of the diffusion phenomena. The method itself can be generalized to design a set of coupled partial differential equations from some assumption about possible reactions between intrinsic point defects and dopants.
Principal ingredients of the diffusion-reaction models are: Fick's diffusion laws, electrical field enhanced diffusion, and species generation and recombination theory.
In the following we will briefly discuss and illustrate each of these basic concepts.
Fick's diffusion laws
The laws of diffusion are mathematical relationships which relate the rate of diffusion to the concentration gradient for net mass transfer.
Such laws are considered to be phenomenological.
We define vector
![]() to be a mass flux of the diffusing component.
In Cartesian
to be a mass flux of the diffusing component.
In Cartesian ![]() coordinates, with the unit coordinates
coordinates, with the unit coordinates
![]() ,
,
![]() and
and
![]() , the mass flux may be written as a vectorial sum:
, the mass flux may be written as a vectorial sum:
where ![]() denotes the diffusion coefficient and
denotes the diffusion coefficient and ![]() is the concentration of the diffusing component.
is the concentration of the diffusing component.
By imposing a mass conservation on the diffusing system we obtain Ficks's second law in the form:
The interpretation of (
![]() ) is clear: If there is a converging flow of species at a point, so that
) is clear: If there is a converging flow of species at a point, so that
![]() , the concentration rises with time; if there is a divergent flow, so that
, the concentration rises with time; if there is a divergent flow, so that
![]() , the concentration falls.
, the concentration falls.
Influence of the Electrical field
We consider a single charged particle moving in the electrical field with potential
![]() . The gradient of this potential describes the force on the particle [18],
. The gradient of this potential describes the force on the particle [18],
| (3.4) |
where ![]() is the valence of the charged species.
A potential gradient tends to produce a flux of the species, and this flux must be added to that produced by the concentration gradient to arrive at the equation for the total flux.
It is found empirically that a potential gradient gives rise to a mean diffusion velocity for the affected atoms. This fact is mathematically expressed by the equation,
is the valence of the charged species.
A potential gradient tends to produce a flux of the species, and this flux must be added to that produced by the concentration gradient to arrive at the equation for the total flux.
It is found empirically that a potential gradient gives rise to a mean diffusion velocity for the affected atoms. This fact is mathematically expressed by the equation,
| (3.5) |
In applying a potential gradient instead of concentration gradient we are simply replacing one small force with another. Thus is plausible that the mobility is proportional to the diffusion coefficient ![]() .
This fact is expressed by Einstein's relationship,
.
This fact is expressed by Einstein's relationship,
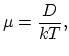 |
(3.6) |
where ![]() is the Boltzmann constant.
The flux that results in a homogenous system is thus,
is the Boltzmann constant.
The flux that results in a homogenous system is thus,
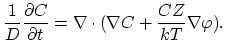 |
(3.8) |
Generally, in the case of non-uniform concentrations of dopants, the electric field calculation is based on third Maxwell's equation,
| (3.10) |
div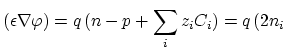 sinh sinh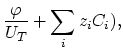 |
(3.11) |
Assuming local charge neutrality,
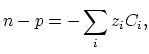 |
(3.12) |
| (3.14) |
| (3.15) |
| (3.16) |
| (3.18) |
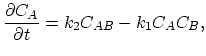 |
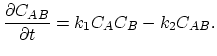 |