

Next: 3.4 Nonequilibrium Models
Up: 3. Diffusion Phenomena in
Previous: 3.2 Interaction of Dopants
Subsections
The models described are valid only when both interstitials and vacancies
remain on their equilibrium levels. All the reactions described in the Sections 3.2.1 and 3.2.2 are also assumed in equilibrium.
Application area of equilibrium diffusion was the modeling of junction formation in the cases where dopants are introduced from the solid source or gas phase into the wafer. However, in all modern process conditions where enhancement of dopant diffusion due to presence of point defects takes place (TED-transient enhanced diffusion), equilibrium diffusion models are very unreliable.
3.3.1 Intrinsic Diffusion
The simplest case of diffusion is the so called intrinsic
diffusion.
The condition where an intrinsic diffusion model can be
applied is when the dopant concentration is low compared to the
intrinsic carrier concentration 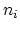 .
This condition has to be fulfilled at
the diffusion temperature under consideration. According to the
empirical fit to the experimental data [23],
.
This condition has to be fulfilled at
the diffusion temperature under consideration. According to the
empirical fit to the experimental data [23],
The governing equation of intrinsic diffusion is,
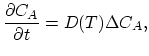 |
(3.30) |
where
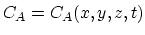 . Under intrinsic doping conditions, the diffusion
coefficient is constant with respect to the dopant concentration.
The temperature dependence of diffusion coefficient determined from experiments is usually found to obey an Arrhenius relation:
. Under intrinsic doping conditions, the diffusion
coefficient is constant with respect to the dopant concentration.
The temperature dependence of diffusion coefficient determined from experiments is usually found to obey an Arrhenius relation:
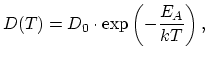 |
(3.31) |
characterized by prefactor 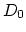 and activation energy
and activation energy 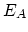 .
The intrinsic diffusion model assumes that dopants diffuse directly
through the silicon grid, passing between the sites of the silicon atoms.
.
The intrinsic diffusion model assumes that dopants diffuse directly
through the silicon grid, passing between the sites of the silicon atoms.
The importance of the intrinsic diffusion model lays in the fact
that it enables to test the basic numerics of the finite element
solver, because in this case an analytic solution of the
diffusion equation is easy to obtain. Secondly, through comparison
with intrinsic diffusion some advanced diffusion models which handle effect such as electric field enahancment and point defects/transient enhancement can be demonstrated.
3.3.2 Extrinsic Diffusion
If the dopant concentration exceeds the intrinsic carrier concentration, an internal electric field is generated.
This electrical field produces a force on the diffusing dopant atoms.
The origin of the field comes from the higher mobility of the electrons and holes compared to dopant atoms.
If we consider the case of an abrupt phosphorus profile, electrons from the donors atoms will tend to diffuse ahead of the profile, because they have a very high mobility.
This leaves behind positively charged phosphorus atoms.
Thus, an electric field is set up which tends to prevent electrons from diffusing further and a steady-state condition exists, when the electron diffusion flux is balanced by the electron drift flux.
The governing equation of extrinsic diffusion is similar to that of intrinsic diffusion, but includes an additional field enhancement factor 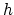 ,
,
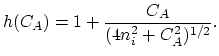 |
(3.32) |
This enhancement factor  can be derived from (3.7)-(3.13).
can be derived from (3.7)-(3.13).
The governing equation of extrinsic diffusion is,
 |
(3.33) |
The extrinsic diffusion model, like the intrinsic difusion model, assumes the direct diffusion mechanism.
3.3.3 Vacancy-Only Assisted Diffusion
Further improvement of the models for diffusion requires to include the specific influence of the point defects' different charge states.
Historically, the most important is the vacancy-only diffusion model [24,6].
For the dopant diffusion via the vacancy mechanism, the diffusion coefficient can be described by,
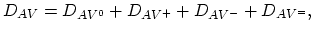 |
(3.34) |
where
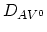 ,
,
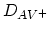 ,
,
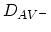 ,
,
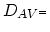 , are the
diffusion coefficients associated with interaction of the impurities
with neutral vacancies, positively charged vacancies, negatively charged vacancies, and doubly
negatively charged vacancies, respectively. The diffusion coefficient
is proportional to the vacancy concentration. Therefore (3.34)
can be expressed as,
, are the
diffusion coefficients associated with interaction of the impurities
with neutral vacancies, positively charged vacancies, negatively charged vacancies, and doubly
negatively charged vacancies, respectively. The diffusion coefficient
is proportional to the vacancy concentration. Therefore (3.34)
can be expressed as,
![$\displaystyle D_{AV}=D_{AV^{0}}^i\Bigl[\frac{C_{V^0}}{C_{V^0}^{i}} \Bigr]+D_{AV...
...}}}{C_{V^{-}}^{i}} \Bigr]+D_{AV^{=}}^i\Bigl[\frac{C_{V^=}}{C_{V^=}^{i}} \Bigr],$](img328.png) |
(3.35) |
where 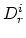 are diffusivities in intrinsic silicon due to
vacancies in charge state "
are diffusivities in intrinsic silicon due to
vacancies in charge state "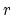 ", and
", and 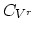 and
and
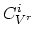 are the vacancies' concentration in the charge state "
are the vacancies' concentration in the charge state "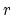 " in extrinsic
silicon and in intrinsic silicon, respectively. Using the law of mass
action in thermal equilibrium, gives,
" in extrinsic
silicon and in intrinsic silicon, respectively. Using the law of mass
action in thermal equilibrium, gives,
![$\displaystyle \frac{C_{V^0}}{C_{V^0}^{i}}=1,\quad \frac{C_{V^{+}}}{C_{V^{+}}^{i...
...c{n}{n_i},\quad \frac{C_{V^{=}}}{C_{V^{=}}^{i}}=\Bigr [\frac{n}{n_i} \Bigl ]^2,$](img332.png) |
(3.36) |
where 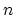 and
and 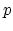 are the free electron and hole
concentrations. Therefore (3.35) becomes under extrinsic
conditions,
are the free electron and hole
concentrations. Therefore (3.35) becomes under extrinsic
conditions,
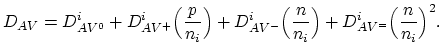 |
(3.37) |
For the diffusion of group III and V dopants of interest, all of
the components associated with various charge states are not
significant.
The governing equation of the model is
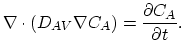 |
(3.38) |
The success of the ``vacancy-only'' theory of dopant diffusion in silicon was initially applied with great enthusiasm to diffusion in silicon.
It had some early dramatic successes, in that it allowed many of the observations of high dopant concentration diffusion to be explained. However, there are still many issues in diffusion, which cannot be handled by ``vacancy-only'' model [24].
It has serious shortcomings and it cannot explain a lot of diffusion phenomena unless the interstitial contribution is also included. For example, the ``vacancy-only'' mechanism cannot explain the emitter-push effect [25], high concentration phosphorus diffusion [26], transient enhanced diffusion [27], and oxidation enhanced or retarded diffusion (OED or ORD) [28].
For these cases diffusion models which include the nonequilibrium dynamics of native point defects are necesarry.



Next: 3.4 Nonequilibrium Models
Up: 3. Diffusion Phenomena in
Previous: 3.2 Interaction of Dopants
H. Ceric: Numerical Techniques in Modern TCAD
![]() .
This condition has to be fulfilled at
the diffusion temperature under consideration. According to the
empirical fit to the experimental data [23],
.
This condition has to be fulfilled at
the diffusion temperature under consideration. According to the
empirical fit to the experimental data [23],
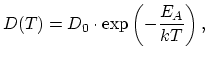
![]() ,
,