next up previous contents
Next: 3.3 Equilibrium Diffusion Up: 3. Diffusion Phenomena in Previous: 3.1 The Physics of

Subsections

3.2 Interaction of Dopants with Simple Native Point Defects

In silicon dopants diffuse via interactions with native point defects. This concept is now generally accepted relying on experimental observations and theoretical calculations [20,21]. The focus of this work is put on interactions with the simple native point defects: interstitial (I) and vacancies (V). A vacancy is an empty lattice site, while an interstitial is a host atom present on a site different from a regular substitutional lattice site.

In the following sections the possible reactions between dopant atoms and native point defects are described. The dopant atom is always denoted as $ A$ and, correspondingly, a vacancy-dopant pair as $ AV$, and an interstitial-dopant pair as $ AI$.


3.2.1 Charge Exchange Reactions

Simple point defects and point defect pairs exists in different charge states. The reactions between charged species and current carriers are expressed by the following relationships for the case of electrons ($ e$),

$\displaystyle I^{i}+e^{-}\Longleftrightarrow I^{i-1},$    

$\displaystyle V^{i}+e^{-}\Longleftrightarrow V^{i-1},$    

$\displaystyle (AI)^{i}+e^{-}\Longleftrightarrow (AI)^{i-1},$ (3.20)

$\displaystyle (AV)^{i}+e^{-}\Longleftrightarrow (AV)^{i-1}.$    

Analogous relations hold also for holes ($ h$). Exponents of the species symbols denote the charge state of the species. Because electronic interactions are much faster than atomic diffusion processes, it is generally assumed that ionization reactions are near equilibrium. In that case, according to (3.20), we can write expressions for the concentrations of each species for each charge state.

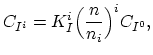$\displaystyle C_{I^i}=K_I^{i}\Bigl(\frac{n}{n_i}\Bigr)^i C_{I^0},$    

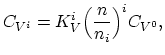$\displaystyle C_{V^i}=K_V^{i}\Bigl(\frac{n}{n_i}\Bigr)^i C_{V^0},$    

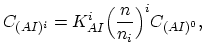$\displaystyle C_{(AI)^i}=K_{AI}^{i}\Bigl(\frac{n}{n_i}\Bigr)^i C_{(AI)^0},$ (3.21)

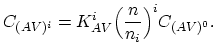$\displaystyle C_{(AV)^i}=K_{AV}^{i}\Bigl(\frac{n}{n_i}\Bigr)^i C_{(AV)^0}.$    

The total concentration of the species is obtained by summation over all charge states of the species. For example for the interstitials $ I$,

$\displaystyle C_{I}=\sum_{i} C_{I^i} = C_{I^0}\sum_{i} \Bigl[ K_I^{i}\Bigl(\frac{n}{n_i}\Bigr)^i\Bigr],$ (3.22)

where $ K_X^{i}$ are equilibrium coefficients.


3.2.2 Dopant and Point Defect Reactions

The system in which a dopant diffuses via interactions with point defects can be described by the following set of reactions. We take as example a reaction with an ionizated $ A^{+}$ donor atom:

dopant-defect pairing reactions,

$\displaystyle A^{+}+I^{i}\Longleftrightarrow (AI)^{i+1},$ (3.23)

$\displaystyle A^{+}+V^{i}\Longleftrightarrow (AV)^{i+1},$ (3.24)


recombination and generation of Frankel pairs,

$\displaystyle I^{i}+V^{j}\Longleftrightarrow (-i-j)e^{-},$ (3.25)


pair dissociation/defect recombination,

$\displaystyle (AI)^{i}+V^{j}\Longleftrightarrow A^{+}+(1-i-j)e^{-},$ (3.26)

$\displaystyle (AV)^{i}+I^{j}\Longleftrightarrow A^{+}+(1-i-j)e^{-},$ (3.27)

$\displaystyle (AV)^{i}+(AI)^{j}\Longleftrightarrow 2 A^{+}+(2-i-j)e^{-}.$ (3.28)

A recombination rate for Frankel pairs can be significantly increased by the last three reactions which represent an alternative for the recombination and generation of vacancies and interstitials at high dopant concentrations [22].

next up previous contents
Next: 3.3 Equilibrium Diffusion Up: 3. Diffusion Phenomena in Previous: 3.1 The Physics of
H. Ceric: Numerical Techniques in Modern TCAD