The physical meaning of the Dirichlet boundary condition is the diffusion from an infinite source of dopants. This might correspond to putting a heavily doped epitaxial layer on a lightly doped wafer.
The Neumann boundary condition for the considered dopant with concentration ![]() ,
,
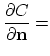 const const |
(3.63) |
Interfaces between different materials occur frequently in silicon processing.
Dopants have different solubilities in different materials and so they redistribute at an interface until the chemical potential is the same on both sides of the interface.
The ratio of the equilibrium doping concentration is defined as the segregation coefficient [31,32].
Next we consider two separate phases ![]() and
and ![]() , which might be oxide and silicon.
The transfer of the single species
, which might be oxide and silicon.
The transfer of the single species ![]() between
between ![]() and
and ![]() having concentrations
having concentrations ![]() in
in ![]() and
and ![]() in
in ![]() is decribed with a basic first order assumption is the species interchange at the interface according to the chemical reaction,
is decribed with a basic first order assumption is the species interchange at the interface according to the chemical reaction,
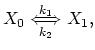 |
(3.64) |
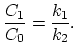 |
(3.66) |
The chemical reaction at the surface of the simulation domain, when a net flux ![]() or
or ![]() of either interstitial or vacancies, respectively is injected, is decribed by the equations,
of either interstitial or vacancies, respectively is injected, is decribed by the equations,
Surface processes are dominant in determining the concentration of point defects in typical silicon wafers [33]. Evidence that pad-oxides/silicon interfaces are good sinks for interstitials comes from observations on the growth and shrinkage of stacking faults in silicon under different surface coverings[34].